
【题目】如图,在底面为等边三角形的斜三棱柱![]() 中,
中, ![]() ,四边形
,四边形![]() 为矩形,过
为矩形,过![]() 作与直线
作与直线![]() 平行的平面
平行的平面![]() 交
交![]() 于点
于点![]() .
.

(1)证明: ![]() ;
;
(2)若直线![]() 与底面
与底面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值 .
的余弦值 .
【答案】(1)见解析(2)![]()
【解析】
(1)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,推导出
,推导出![]() ,由四边形
,由四边形![]() 为平行四边形,得
为平行四边形,得![]() 为
为![]() 的中位线,从而
的中位线,从而![]() 为
为![]() 的中点,由此能证明
的中点,由此能证明![]() ;
;
(2)过![]() 作
作![]() 平面
平面![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,以
,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 的方向为
的方向为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向建立空间直角坐标系,利用向量法能求出二面角
轴的正方向建立空间直角坐标系,利用向量法能求出二面角![]() 的余弦值.
的余弦值.
解:(1)如图,
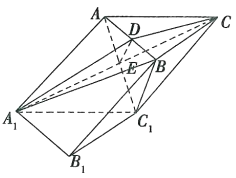
连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
因为![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]()
平面![]() ,所以
,所以![]() .
.
又四边形![]() 为平行四边形,
为平行四边形,
所以![]() 为
为![]() 的中点,所以
的中点,所以![]() 为
为![]() 的中位线,所以
的中位线,所以![]() 为
为![]() 的中点.
的中点.
又![]() 为等边三角形,所以
为等边三角形,所以![]() .
.
(2)过![]() 作
作![]() 平面
平面![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,设
,设![]() ,
,
则![]() .
.
因为直线![]() 与底面
与底面![]() 所成的角为
所成的角为![]() ,所以
,所以![]() .
.
在![]() 中,因为
中,因为![]() ,
,
所以![]() ,
,![]() .
.
为![]() 平面
平面![]() 平面
平面![]() ,
,
所以![]() ,
,
四边形![]() 为矩形,所以
为矩形,所以![]() ,
,
因为![]() ,所以
,所以![]() .
.
因为![]() 平面
平面![]() 平面
平面![]() ,所以
,所以
![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
又![]() 为等边三角形,所以
为等边三角形,所以![]() 为
为![]() 的中点.
的中点.
以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 的方向为
的方向为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向建立空间直角坐标系,如图.
轴的正方向建立空间直角坐标系,如图.
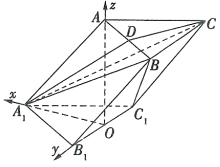
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
因为![]() ,
,
所以![]() ,
,
因为![]() ,
,
所以![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
设平面![]() 的法向量为
的法向量为![]() .
.
由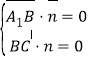 ,得
,得![]() ,
,
令![]() ,得
,得![]() ,
,
所以平面![]() 的一个法向量为
的一个法向量为![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由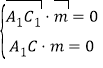 ,得
,得![]() ,
,
令![]() ,得
,得![]() ,
,
所以平面![]() 的一个法向量为
的一个法向量为![]() .
.
所以![]() ,
,
因为所求二面角为钝角,所以二面角![]() 的余弦值为
的余弦值为![]() .
.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )
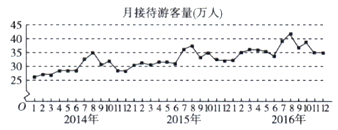
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .将
.将![]() 的图象向左平移
的图象向左平移![]() 个单位长度后所得的函数为偶函数,则关于函数
个单位长度后所得的函数为偶函数,则关于函数![]() ,下列命题正确的是( )
,下列命题正确的是( )
A. 函数![]() 在区间
在区间![]() 上有最小值 B. 函数
上有最小值 B. 函数![]() 在区间
在区间![]() 上单调递增
上单调递增
C. 函数![]() 的一条对称轴为
的一条对称轴为![]() D. 函数
D. 函数![]() 的一个对称点为
的一个对称点为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|2≤x≤8},B={x|1<x<6},C={x|x>a},U=R.
(1)求A∪B,(CUA)∩B;
(2)若A∩C≠![]() ,求a的取值范围.
,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司将进货单价为8元一个的商品按10元一个出售,每天可以卖出100个,若这种商品的售价每个上涨1元,则销售量就减少10个.
(1)求售价为13元时每天的销售利润;
(2)求售价定为多少元时,每天的销售利润最大,并求最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数:f(x)=x2﹣mx﹣n(m, n∈R).
(1)若m+n=0,解关于x的不等式f(x)≥x(结果用含m式子表示);
(2)若存在实数m,使得当x∈[1,2]时,不等式x≤f(x)≤4x恒成立,求实数n的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为比较注射![]() 两种药物产生的皮肤疱疹的面积,选200只家兔作试验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物
两种药物产生的皮肤疱疹的面积,选200只家兔作试验,将这200只家兔随机地分成两组,每组100只,其中一组注射药物![]() ,另一组注射药物
,另一组注射药物![]() .表1和表2所示的分别是注射药物
.表1和表2所示的分别是注射药物![]() 和药物
和药物![]() 后皮肤疱疹面积的频数分布(疱疹面积单位:
后皮肤疱疹面积的频数分布(疱疹面积单位:![]() )
)
表1
疱疹面积 |
|
|
|
|
频数 | 30 | 40 | 20 | 10 |
表2
疱疹面积 |
|
|
|
|
|
频数 | 10 | 25 | 20 | 30 | 15 |
(1)完成图20-3和图20-4所示的分别注射药物![]() 后皮肤疱疹面积的频率分布直方图,并求注射药物
后皮肤疱疹面积的频率分布直方图,并求注射药物![]() 后疱疹面积的中位数
后疱疹面积的中位数

(2)完成下表所示的![]() 列联表,并回答能否有99.9%的把握认为注射药物
列联表,并回答能否有99.9%的把握认为注射药物![]() 后的疱疹面积与注射药物
后的疱疹面积与注射药物![]() 的疱疹面积有差异.(
的疱疹面积有差异.(![]() 的值精确到0.01)
的值精确到0.01)
疱疹面积小于 | 疱疹面积不小于 | 合计 | |
注射药物A |
|
| |
注射药物B |
|
| |
合计 |
附: .
.
P( | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.811 | 5.021 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com