
科目:高中数学 来源:不详 题型:解答题
| | 患心肺疾病 | 不患心肺疾病 | 合计 |
| 大于40岁 | 16 | | |
| 小于等于40岁 | | 12 | |
| 合计 | | | 40 |

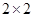 列联表补充完整;
列联表补充完整;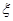 ,求
,求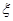 的分布列和数学期望;
的分布列和数学期望;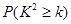 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
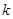 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
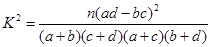 ,其中
,其中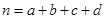 )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 在一段线路中并联着3个自动控制的常开开关,只要其中一个开关能够闭合,线路就能正常工作,假定在某段时间内,每个开关能够闭合的概率都是0.7,计算在这段时间内:
在一段线路中并联着3个自动控制的常开开关,只要其中一个开关能够闭合,线路就能正常工作,假定在某段时间内,每个开关能够闭合的概率都是0.7,计算在这段时间内:查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
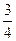 ,甲、丙两人都回答错误的概率是
,甲、丙两人都回答错误的概率是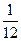 ,乙、丙两人都回答对的概率是
,乙、丙两人都回答对的概率是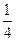 .
. 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.无论采用哪种方法,这150个教工中每一个被抽到的概率都相等 |
| B.①②两种抽样方法,这150个教工中每一个被抽到的概率都相等;③并非如此 |
| C.①③两种抽样方法,这150个教工中每一个被抽到的概率都相等;②并非如此 |
| D.采用不同的抽样方法,这150个教工中每一个被抽到的概率是各不相同的 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 病症及代号 | 普通病症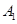 | 复诊病症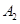 | 常见病症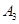 | 疑难病症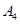 | 特殊病症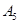 |
| 人数 | 100 | 300 | 200 | 300 | 100 |
| 每人就诊时间(单位:分钟) | 3 | 4 | 5 | 6 | 7 |
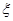 表示某病人诊断所需时间,求
表示某病人诊断所需时间,求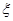 的数学期望.
的数学期望.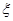 ,求
,求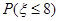 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
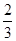 。
。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com