
【题目】为了调查甲、乙两个网站受欢迎的程度,随机选取了14天,统计上午8:00~10:00各自的点击量,得到如图所示的茎叶图,根据茎叶图回答下列问题.

(1)甲、乙两个网站点击量的极差分别是多少?
(2)甲网站点击量在[10,40]间的频率是多少?
(3)甲、乙两网站哪个更受欢迎?并说明理由.
【答案】(1)65,66; (2)0.286; (3) 甲网站更受欢迎
【解析】
(1)根据茎叶图,得到甲乙两网站的最大点击量和最小点击量,即可求解极差;
(2)由茎叶图可知,在![]() 中,有
中,有![]() ,共4个数据,即可求解相应的概率;
,共4个数据,即可求解相应的概率;
(3)由茎叶图,可知甲网站的点击量集中在茎叶图的下方,而乙网站的点击量集中在茎叶图的上方,即可作出判定.
(1)由茎叶图可知,
甲网站最大点击量为73,最小的点击量为8,所以甲网站的点击量的极差为73–8=65,
乙网站最大点击量为71,最小的点击量为5,所以乙网站的点击量的极差为71–5=66.
(2)由茎叶图可知,在![]() 中,有
中,有![]() ,共4个数据,
,共4个数据,
所以甲网站在![]() 内的概率为
内的概率为![]() .
.
(3)由茎叶图,可知甲网站的点击量集中在茎叶图的下方,而乙网站的点击量集中在茎叶图的上方,从数据的分布情况来看,可判定甲网站更受欢迎.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的极小值;
的极小值;
(2)若函数![]() 在
在![]() 有
有![]() 个零点,求实数
个零点,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若函数![]() 在
在![]() 的三个零点分别为
的三个零点分别为![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,D是 ![]() 的中点,BD交AC于E. (Ⅰ)求证:DC2=DEDB;
的中点,BD交AC于E. (Ⅰ)求证:DC2=DEDB;
(Ⅱ)若CD=2 ![]() ,O到AC的距离为1,求⊙O的半径r.
,O到AC的距离为1,求⊙O的半径r.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x||x﹣1|≤2,x∈Z},B={x|y=log2(x+1),x∈R},则A∩B=( )
A.{﹣1,0,1,2,3}
B.{0,1,2,3}
C.{1,2,3}
D.{﹣1,1,2,3}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面ABCD是矩形,
中,底面ABCD是矩形,![]() 平面ABCD,
平面ABCD,![]() ,E,F是线段BC,AB的中点.
,E,F是线段BC,AB的中点.

![]() Ⅰ
Ⅰ![]() 证明:
证明:![]() ;
;
![]() Ⅱ
Ⅱ![]() 在线段PA上确定点G,使得
在线段PA上确定点G,使得![]() 平面PED,请说明理由.
平面PED,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某算法的程序框图如图所示,若将输出的(x,y)值依次记为(x1,y1),(x2,y2),…,(xn,yn),….
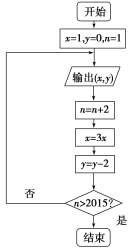
(1)若程序运行中输出的一个数组是(9,t),求t的值;
(2)程序结束时,共输出(x,y)的组数为多少;
(3)写出程序框图的程序语句.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A、B、C三位老师分别教数学、英语、体育、劳技、语文、阅读六门课,每位教两门.已知:
(1)体育老师和数学老师住在一起,
(2)A老师是三位老师中最年轻的,
(3)数学老师经常与C老师下象棋,
(4)英语老师比劳技老师年长,比B老师年轻,
(5)三位老师中最年长的老师比其他两位老师家离学校远.
问:A、B、C三位老师每人各教哪几门课?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四面体![]() 中,
中, ![]() 在平面
在平面![]() 的射影
的射影![]() 为棱
为棱![]() 的中点,
的中点, ![]() 为棱
为棱![]() 的中点,过直线
的中点,过直线![]() 作一个平面与平面
作一个平面与平面![]() 平行,且与
平行,且与![]() 交于点
交于点![]() ,已知
,已知![]() ,
, ![]() .
.

(1)证明: ![]() 为线段
为线段![]() 的中点
的中点
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均不相等的等差数列{an}的前四项和S4=14,且a1 , a3 , a7成等比数列. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)设Tn为数列{ ![]() }的前n项和,若Tn≤λan+1对n∈N*恒成立,求实数λ的最小值.
}的前n项和,若Tn≤λan+1对n∈N*恒成立,求实数λ的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com