
【题目】根据下列条件分别写出直线的方程,并化为一般式方程:
(1)斜率是![]() ,且经过点A(5,3) 的直线方程为___________
,且经过点A(5,3) 的直线方程为___________
(2)斜率为4,在y轴上的截距为-2的直线方程为__________
(3)经过点A(-1,5),B(2,-1)两点的直线方程为____________
(4)在x轴,y轴上的截距分别为-3,-1的直线方程为___________
(5)斜率是-![]() ,且经过点A(8,-6)的直线方程为_________
,且经过点A(8,-6)的直线方程为_________
(6)经过点B(4,2),且平行于x轴的直线方程为__________
(7)在x轴和y轴上的截距分别是![]() 和-3的直线方程为_________
和-3的直线方程为_________
(8)经过点P1(3,-2),P2(5,-4)的直线方程为__________
【答案】 ![]() x-y-5
x-y-5![]() +3=0. 4x-y-2=0. 2x+y-3=0. 2x+y-3=0. x+2y+4=0. y-2=0. 2x-y-3=0. x+y-1=0.
+3=0. 4x-y-2=0. 2x+y-3=0. 2x+y-3=0. x+2y+4=0. y-2=0. 2x-y-3=0. x+y-1=0.
【解析】
根据直线方程的形式:点斜式、斜截式、两点式和截距式方程的形式,即可求解所求直线的方程.
(1)由直线的点斜式方程可知,所求直线的方程为![]() ,
,
即所求直线的方程为![]() ;
;
(2)由直线的截距式方程可知,所求直线的方程为![]() ,即所求方程为
,即所求方程为![]() ;
;
(3)由直线的两点式方程可知,所求直线的方程为![]() ,
,
即所求直线的方程为![]() ;
;
(4)由直线的截距式方程可知,所求直线的方程为![]() ,
,
即所求直线的方程为![]() ;
;
(5)由直线的点斜式方程可知,所求直线的方程为![]() ,
,
即所求直线的方程为![]() ;
;
(6)由题意,直线平行于![]() 轴,所以斜率
轴,所以斜率![]() ,所以所求方程为
,所以所求方程为![]() ;
;
(7)由直线的截距式方程可知,所求直线的方程为![]() ,
,
即所求直线的方程为![]() ;
;
(8)由直线的两点式方程可知,所求直线的方程为![]() ,
,
即所求直线的方程为![]() ;
;


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案科目:高中数学 来源: 题型:
【题目】(本题满分10分)已知等差数列{an}满足a1+a2=10,a4-a3=2.
(1)求{an}的通项公式.
(2)设等比数列{bn}满足b2=a3,b3=a7.问:b6与数列{an}的第几项相等?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了增强消防安全意识,某中学对全体学生做了一次消防知识讲座,从男生中随机抽取50人,从女生中随机抽取70人参加消防知识测试,统计数据得到如下列联表:
优秀 | 非优秀 | 总计 | |
男生 | 15 | 35 | 50 |
女生 | 30 | 40 | 70 |
总计 | 45 | 75 | 120 |
(Ⅰ)试判断是否有![]() 的把握认为消防知识的测试成绩优秀与否与性别有关;
的把握认为消防知识的测试成绩优秀与否与性别有关;
附:
K2=![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(Ⅱ)为了宣传消防安全知识,从该校测试成绩获得优秀的同学中采用分层抽样的方法,随机选出6名组成宣传小组,现从这6人中随机抽取2名到校外宣传,求到校外宣传的同学中至少有1名是男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中装有红球3个、白球2个、黑球1个,从中任取2个,则互斥而不对立的两个事件是( )
A. 至少有一个白球;至少有一个红球 B. 至少有一个白球;红、黑球各一个
C. 恰有一个白球;一个白球一个黑球 D. 至少有一个白球;都是白球
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[100,110),[110,120),[120,130)三组内的学生中,用分层抽样的方法选取28人参加一项活动,则从身高在[120,130)内的学生中选取的人数应为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(ax+ ![]() )+
)+ ![]() .
.
(1)若a>0,且f(x)在(0,+∞)上单调递增,求实数a的取值范围;
(2)是否存在实数a,使得函数f(x)在(0,+∞)上的最小值为1?若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为
的棱长为![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为线段
为线段![]() 上的动点,过点
上的动点,过点![]() ,
, ![]() ,
, ![]() 的平面截该正方体所得的截面为
的平面截该正方体所得的截面为![]() ,则下列命题正确的是__________(写出所有正确命题的编号).
,则下列命题正确的是__________(写出所有正确命题的编号).
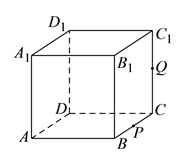
①当![]() 时,
时, ![]() 为四边形;②当
为四边形;②当![]() 时,
时, ![]() 为等腰梯形;
为等腰梯形;
③当![]() 时,
时, ![]() 与
与![]() 的交点
的交点![]() 满足
满足![]() ;
;
④当![]() 时,
时, ![]() 为五边形;
为五边形;
⑤当![]() 时,
时, ![]() 的面积为
的面积为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com