考点:直线与平面所成的角,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)证明BC⊥AB
1,A
1B⊥AB
1,利用直线与平面垂直的判定定理证明AB
1⊥平面A
1BC.
(2)解法一:设AB
1∩A
1B=O,连结CO,说明∠ACO就是直线AC与平面A
1BC所成的角θ,在Rt△AOC中,求解直线AC与平面A
1BC所成的角.
解法二:由(1)知以B为原点建立如图所示坐标系B-xyz,设BC=x,求出B,A,C,A
1,求出
=(2,-2,0),
,直线AC与平面A
1BC所成的角为θ,利用向量的数量积求解即可.
解答:
解:(1)证明:∵在直三棱柱ABC-A
1B
1C
1中,
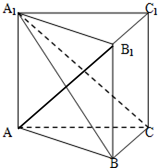
在直三棱柱ABC-A
1B
1C
1(侧棱垂直于底面)中,BC⊥AB,且AA
1=AB=2.
∴A
1A⊥面ABC,…..(1分),BC?面ABC
∴A
1A⊥BC …..(2分)
又∵BC⊥AB…..(3分),
AB∩AA
1=A,
∴
BC⊥平面AA1B,(4分)
平面AB
1?平面ABB
1A,
∴BC⊥AB
1,(5分)
∵四边形A
1ABB
1是正方形,
∴A
1B⊥AB
1…..(6分)
又∵BC∩A
1B=B,AB
1⊥平面A
1BC;…..(7分)
(2)解法一:设AB
1∩A
1B=O,连结CO
…(8分),
∵BC⊥平面A
1ABB
1.则∠ACO就是直线AC与平面A
1BC所成的角θ…(10分)
∵BC=2,∵
AO=AB1=;
sin∠ACO=sinθ=…..(11分)
∴
AC═2,AO=…..(12分)
在Rt△AOC中,
sinθ=,∴θ=
…..(13分)∴BC的长为2时,直线AC与平面A
1BC所成的角为
.…..(14分)
解法二:由(1)知以B为原点建立如图所示坐标系B-xyz,
…(8分),
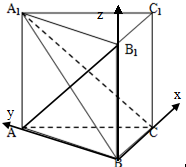
设BC=x,则B(0,0,0),A(0,2,0),C(2,0,0)A
1(0,2,2),
…(10分),
由(1)知AB
1⊥平面A
1BC
,…(11分),
B
1(0,0,2),
=(0,-2,2),…(12分),
∵直线AC与平面A
1BC所成的角为θ,
∴
sinθ=|cos<,>|=||=,…(13分)
即BC的长为2时,直线AC与平面A
1BC所成的角为
.…..(14分)
点评:本题考查直线与平面垂直的判定定理的应用,直线与平面所成角的求法,考查计算能力以及逻辑推理能力.

 如图,在直三棱柱ABC-A1B1C1(侧棱垂直于底面)中,BC⊥AB,且AA1=AB=2.
如图,在直三棱柱ABC-A1B1C1(侧棱垂直于底面)中,BC⊥AB,且AA1=AB=2. 在直三棱柱ABC-A1B1C1(侧棱垂直于底面)中,BC⊥AB,且AA1=AB=2.
在直三棱柱ABC-A1B1C1(侧棱垂直于底面)中,BC⊥AB,且AA1=AB=2.


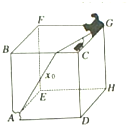 一位电脑爱好者设计了一个“猫捉老鼠”的动画游戏,如图所示,在一个边长为a的大正方体木箱的一个顶点G上,老鼠从猫的爪间逃出,沿着木箱的棱边奔向洞口,洞口子在方木箱的另一顶点A处,若老鼠在奔跑中,并不重复跳过任意一条棱边,也不再回到G点,聪明的猫也选择了一条最短的路程奔向洞口(设猫和老鼠同时从G点出发),结果猫再次在洞口A捉住了老鼠,问:
一位电脑爱好者设计了一个“猫捉老鼠”的动画游戏,如图所示,在一个边长为a的大正方体木箱的一个顶点G上,老鼠从猫的爪间逃出,沿着木箱的棱边奔向洞口,洞口子在方木箱的另一顶点A处,若老鼠在奔跑中,并不重复跳过任意一条棱边,也不再回到G点,聪明的猫也选择了一条最短的路程奔向洞口(设猫和老鼠同时从G点出发),结果猫再次在洞口A捉住了老鼠,问: