
【题目】按照《国务院关于印发“十三五”节能减排综合工作方案的通知》(国发[2016〕74号)的要求,到2020年,全国化学需氧量排放总量要控制在2001万吨以内,要比2015年下降10%假设“十三五”期间每一年化学需氧量排放总量下降的百分比都相等,2015年后第![]() 年的化学需氧量排放总量最大值为
年的化学需氧量排放总量最大值为![]() 万吨.
万吨.
(1)求![]() 的解析式;
的解析式;
(2)求2019年全国化学需氧量排放总量要控制在多少万吨以内(精确到1万吨).
科目:高中数学 来源: 题型:
【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸
与尺寸![]() 之间近似满足关系式
之间近似满足关系式![]() 为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间
为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品.现随机抽取6件合格产品,测得数据如下:
内时为优等品.现随机抽取6件合格产品,测得数据如下:
尺寸 | 38 | 48 | 58 | 68 | 78 | 88 |
质量 | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
质量与尺寸的比 | 0.442 | 0.392 | 0.357 | 0.329 | 0.308 | 0.290 |
(Ⅰ)现从抽取的6件合格产品中再任选3件,求恰好取到2件优等品的概率;
(Ⅱ)根据测得数据作了初步处理,得相关统计量的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(i)根据所给统计量,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(ii)已知优等品的收益![]() (单位:千元)与
(单位:千元)与![]() 的关系
的关系![]() ,则当优等品的尺寸为
,则当优等品的尺寸为![]() 为何值时,收益
为何值时,收益![]() 的预报值最大?(精确到0.1)
的预报值最大?(精确到0.1)
附:对于样本![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高一新生对文理科的选择,对1 000名高一新生发放文理科选择调查表,统计知,有600名学生选择理科,400名学生选择文科.分别从选择理科和文科的学生随机各抽取20名学生的数学成绩得如下累计表:
分数段 | 理科人数 | 文科人数 |
|
| |
|
| |
|
|
|
| 正 | 正 |
| 正 |
|
|
|
|
(1)从统计表分析,比较选择文理科学生的数学平均分及学生选择文理科的情况,并绘制理科数学成绩的频率分布直方图.

(2)根据你绘制的频率分布直方图,估计意向选择理科的学生的数学成绩的中位数与平均分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() ,如图.
,如图.
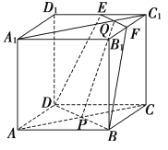
(1)若![]() 交平面
交平面![]() 于点
于点![]() ,证明:
,证明:![]() 、
、![]() 、
、![]() 三点共线;
三点共线;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ,若存在确定
,若存在确定![]() 的位置,若不存在说明理由.
的位置,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把物体放在冷空气中冷却,如果物体原来的温度是![]() ,空气的温度是
,空气的温度是![]() ,则1min后物体的温度
,则1min后物体的温度![]() 可由公式
可由公式![]() 求得,其中k是常数,把温度是
求得,其中k是常数,把温度是![]() 的物体放在15℃的空气中冷却,1 min后,物体的温度是
的物体放在15℃的空气中冷却,1 min后,物体的温度是![]() .
.
(1)求出k的值;
(2)计算开始冷却多久后,上述物体的温度分别是![]() ;
;
(3)判断上述物体最终能否冷却到12℃,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在等比数列{an}中,![]() =2,,
=2,,![]() =128,数列{bn}满足b1=1,b2=2,且{
=128,数列{bn}满足b1=1,b2=2,且{![]() }为等差数列.
}为等差数列.
(1)求数列{an}和{bn}的通项公式;
(2)求数列{bn}的前n项和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com