
【题目】甲、乙、丙三人独立的对某一技术难题进行攻关。甲能攻克的概率为![]() ,乙能攻克的概率为
,乙能攻克的概率为![]() ,丙能攻克的概率为
,丙能攻克的概率为![]() ;
;
(1)求这一技术难题被攻克的概率;
(2)若该技术难题未被攻克,上级不做任何奖励;若该技术难题被攻克,上级会奖励6万元。奖励规则如下:若只有一人攻克,则此人获得全部奖金6万元;若只有2人攻克,则此二人均分奖金,每人3万元;若三人均攻克,则每人2万元。在这一技术难题被攻克的前提下,设甲拿到的奖金数为![]() ,求
,求![]() 的分布列和数学期望。
的分布列和数学期望。
科目:高中数学 来源: 题型:
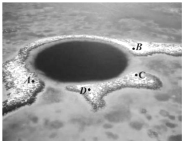
【题目】海洋蓝洞是地球罕见的自然地理现象,被喻为“地球留给人类保留宇宙秘密的最后遗产”,我国拥有世界上最深的海洋蓝洞,若要测量如图所示的蓝洞的口径![]() ,
,![]() 两点间的距离,现在珊瑚群岛上取两点
两点间的距离,现在珊瑚群岛上取两点![]() ,
,![]() ,测得
,测得![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() 两点的距离为___.
两点的距离为___.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙3位大学生同时应聘某个用人单位的职位,甲、乙两人只有一人被选中的概率为![]() ,两人都被选中的概率为
,两人都被选中的概率为![]() ,丙被选中的概率为
,丙被选中的概率为![]() ,且三人各自能否被选中互不影响.
,且三人各自能否被选中互不影响.
(1)求3人同时被选中的概率;
(2)求恰好有2人被选中的概率;
(3)求3人中至少有1人被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列两组数据:甲:12,13,11,10,14.乙:10,17,10,13,10.
(1)分别计算两组数据的平均差,并根据计算结果判断哪组数据波动大.
(2)分别计算两组数据的方差,并根据计算结果判断哪组数据波动大.
(3)以上两种判断方法的结果是否一致?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们国家正处于老龄化社会中,老有所依也是政府的民生工程.某市共有户籍人口400万,其中老人(年龄60岁及以上)人数约有66万,为了了解老人们的健康状况,政府从老人中随机抽取600人并委托医疗机构免费为他们进行健康评估,健康状况共分为不能自理、不健康尚能自理、基本健康、健康四个等级,并以80岁为界限分成两个群体进行统计,样本分布被制作成如下图表:
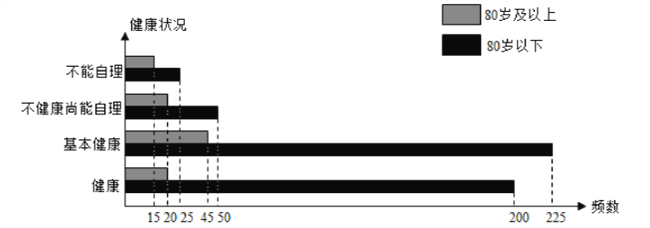
(1)若采用分层抽样的方法再从样本中的不能自理的老人中抽取8人进一步了解他们的生活状况,则两个群体中各应抽取多少人?
(2)估算该市80岁及以上长者占全市户籍人口的百分比;
(3)据统计该市大约有五分之一的户籍老人无固定收入,政府计划为这部分老人每月发放生活补贴,标准如下:
①80岁及以上长者每人每月发放生活补贴200元;
②80岁以下老人每人每月发放生活补贴120元;
③不能自理的老人每人每月额外发放生活补贴100元.
利用样本估计总体,试估计政府执行此计划的年度预算.(单位:亿元,结果保留两位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两名学生中选拔一人参加射击比赛,对他们的射击水平进行了测试,两人在相同条件下各射击10次,命中的环数如下:
甲:7,8,6,9,6,5,9,9,7,4.
乙:9,5,7,8,7,6,8,6,7,7.
(1)分别计算甲、乙两人射击命中环数的极差、众数和中位数;
(2)分别计算甲、乙两人射击命中环数的平均数、方差、标准差;
(3)比较两人的成绩,然后决定选择哪一个人参赛.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义域为![]() 的函数
的函数![]() 同时满足以下三条:
同时满足以下三条:
(ⅰ)对任意的![]() 总有
总有![]() (ⅱ)
(ⅱ)![]()
(ⅲ)若![]() 则有
则有![]() 就称
就称![]() 为“A函数”,下列定义在
为“A函数”,下列定义在![]() 的函数中为“A函数”的有_______________
的函数中为“A函数”的有_______________
①![]() ;②
;②![]() ③
③![]() ④
④![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从![]() 年
年![]() 月份,某市街头出现共享单车,到
月份,某市街头出现共享单车,到![]() 月份,根据统计,市区所有人骑行过共享单车的人数已占
月份,根据统计,市区所有人骑行过共享单车的人数已占![]() ,骑行过共享单车的人数中,有
,骑行过共享单车的人数中,有![]() 是大学生(含大中专及高职),该市区人口按
是大学生(含大中专及高职),该市区人口按![]() 万计算,大学生人数约
万计算,大学生人数约![]() 万人.
万人.
(1)任选出一名大学生,求他(她)骑行过共享单车的概率;
(2)随单车投放数量增加,乱停乱放成为城市管理的问题,以下是累计投放单车数量![]() 与乱停乱放单车数量
与乱停乱放单车数量![]() 之间的关系图表:
之间的关系图表:
累计投放单车数量 |
|
|
|
|
|
乱停乱放单车数量 |
|
|
|
|
|
①计算![]() 关于
关于![]() 的线性回归方程(其中
的线性回归方程(其中![]() 精确到
精确到![]() 值保留三位有效数字),并预测当
值保留三位有效数字),并预测当![]() 时,单车乱停乱放的数量;
时,单车乱停乱放的数量;
②已知该市共有五个区,其中有两个区的单车乱停乱放数量超过标准.在“双创”活动中,检查组随机抽取三个区调查单车乱停乱放数量, ![]() 表示“单车乱停乱放数量超过标准的区的个数”,求
表示“单车乱停乱放数量超过标准的区的个数”,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
参考公式和数据:回归直线方程![]() 中的斜率和截距的最小二乘法估计公式分别为
中的斜率和截距的最小二乘法估计公式分别为
![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com