
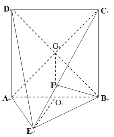
【题目】如图,直二面角D—AB—E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.

(1)求证:AE⊥平面BCE;
(2)求二面角B—AC—E的余弦值.
【答案】(1)详见解析(2)![]()
【解析】
试题分析:(1)欲证AE⊥平面BCE,由题设条件知可先证BF⊥AE,CB⊥AE,再由线面垂直的判定定理得出线面垂直即可;(2)求二面角B-AC-E的正弦值,需要先作角,连接BD交AC交于G,连接FG,可证得∠BGF是二面B-AC-E的平面角,在△BFG中求解即可
试题解析:(1)证明:∵![]() 平面ACE.
平面ACE.![]()
![]() ------------------1分
------------------1分
∵二面角D—AB—E为直二面角,且![]() ,
,
![]() ,
,![]()
![]() 平面ABE ------------------3分
平面ABE ------------------3分

![]()
![]() ------------------4分
------------------4分
又∵BF∩CB=B,![]()
![]() ------------------5分
------------------5分
(2)解:连结BD交AC于G,连结FG.
∵![]() 平面ACE,∴
平面ACE,∴![]() AC
AC
又∵正方形ABCD中,![]() ,且BF∩BG=B
,且BF∩BG=B
∴![]()
![]()
![]() 即为二面角B—AC—E的平面角------------------8分
即为二面角B—AC—E的平面角------------------8分
∵![]() ,
,![]() ,
,![]() ,
,
在![]() 中,可求
中,可求![]()
![]() ,
,
∴在![]() 中,FG=
中,FG=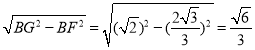
∴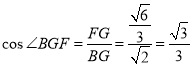 ,即二面角B—AC—E的余弦值为
,即二面角B—AC—E的余弦值为![]() ------------12分
------------12分


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x)万元,当年产量不足80千件时,C(x)=![]() x2+10x(万元);当年产量不少于80千件时,C(x)=51x+
x2+10x(万元);当年产量不少于80千件时,C(x)=51x+![]() -1 450(万元).通过市场分析,若每件售价为500元时,该厂年内生产的商品能全部销售完.
-1 450(万元).通过市场分析,若每件售价为500元时,该厂年内生产的商品能全部销售完.
(1)写出年利润L(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的定义域;
的定义域;
(2)若![]() ,判断
,判断![]() 的奇偶性;
的奇偶性;
(3)是否存在实数![]() ,使函数
,使函数![]() 在
在![]() 递增,并且最大值为1,若存在,求出
递增,并且最大值为1,若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣3x+2≤0},集合B={y|y=x2﹣2x+a},集合C={x|x2﹣ax﹣4≤0},命题p:A∩B≠![]() ,命题q:A
,命题q:A![]() C.
C.
(1)若命题p为假命题,求实数a的取值范围.
(2)若命题p∧q为真命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的最小值为
的最小值为![]() ,且
,且![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若![]() 在区间
在区间![]() 上不单调,求实数
上不单调,求实数![]() 的取值范围;
的取值范围;
(3)在区间![]() 上,
上,![]() 的图象恒在
的图象恒在![]() 的图象上方,试确定实数
的图象上方,试确定实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】统计表明,某种型号的汽车在匀速行驶中每小时的耗油量![]() (升)关于行驶速度
(升)关于行驶速度![]() (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为:![]() .已知甲、乙两地相距100千米.
.已知甲、乙两地相距100千米.
(Ⅰ)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(II)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com