
【题目】已知圆C过点![]() ,且与圆
,且与圆![]() 外切于点
外切于点![]() ,
,![]() 是x轴上的一个动点.
是x轴上的一个动点.
![]() 求圆C的标准方程;
求圆C的标准方程;
![]() 当圆C上存在点Q,使
当圆C上存在点Q,使![]() ,求实数m的取值范围;
,求实数m的取值范围;
![]() 当
当![]() 时,过P作直线PA,PB与圆C分别交于异于点P的点A,B两点,且
时,过P作直线PA,PB与圆C分别交于异于点P的点A,B两点,且![]() 求证:直线AB恒过定点.
求证:直线AB恒过定点.
【答案】(1)![]() (2)
(2)![]() (3)直线AB恒过定点
(3)直线AB恒过定点![]() .
.
【解析】
1)设出圆的标准方程x2+(y﹣b)2=r2,由已知可得关于r,b的方程组求解得答案;
(2)把圆C上存在点Q,使∠CPQ=30°,转化为直线y=![]() (x﹣m)与圆C有交点,由圆心到直线的距离小于半径求解;
(x﹣m)与圆C有交点,由圆心到直线的距离小于半径求解;
(3)m=1时,P(1,0),设kPA=k,则kPB=![]() ,可得直线PA,PB的方程,与圆的方程联立,求得A,B的坐标,写出AB所在直线方程,分别取k=1和﹣1,得到直线方程,联立求得交点坐标,再代回直线方程验证得答案.
,可得直线PA,PB的方程,与圆的方程联立,求得A,B的坐标,写出AB所在直线方程,分别取k=1和﹣1,得到直线方程,联立求得交点坐标,再代回直线方程验证得答案.
![]() 设圆C:
设圆C:![]() ,
,
则![]() ,解得,
,解得,![]() ,
,![]() ,
,
故圆C的标准方程为:![]() ;
;
![]() 解:当圆C上存在点Q,使
解:当圆C上存在点Q,使![]() ,等价于直线
,等价于直线![]() 与圆C有交点,
与圆C有交点,
![]() 圆C到直线
圆C到直线![]() 的距离小于等于半径1,
的距离小于等于半径1,
即![]() ,解得
,解得![]() ,
,
故实数m的取值范围是![]() ;
;
![]() 证明:
证明:![]() 时,
时,![]() ,设
,设![]() ,则
,则![]() ,
,
则直线PA:![]() ,PB:
,PB:![]() ,
,
联立![]() ,得
,得![]() ,
,
则![]() ,得
,得![]() ,
,![]() .
.
![]() ,
,
同理可得![]()
则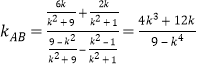 .
.
![]() 直线AB的方程为
直线AB的方程为![]()
当![]() 时,直线方程为
时,直线方程为![]() ,当
,当![]() 时,直线方程为
时,直线方程为![]() .
.
联立![]() ,解得
,解得![]() ,
,![]() .
.
把点![]() 代入
代入![]() 成立,
成立,
![]() 直线AB恒过定点
直线AB恒过定点![]() .
.


科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.

(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】考拉兹猜想又名3n+1猜想,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能得到1.阅读如图所示的程序框图,运行相应程序,输出的结果i=( ) 
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,且过点
,且过点 ![]() .若点M(x0 , y0)在椭圆C上,则点
.若点M(x0 , y0)在椭圆C上,则点 ![]() 称为点M的一个“椭点”.
称为点M的一个“椭点”.
(1)求椭圆C的标准方程;
(2)若直线l:y=kx+m与椭圆C相交于A,B两点,且A,B两点的“椭点”分别为P,Q,以PQ为直径的圆经过坐标原点,试求△AOB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公比不等于1的等比数列{an},满足:a3=3,S3=9,其中Sn为数列{an}的前n项和.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=log2![]() , 若cn=
, 若cn=![]() , 求数列{cn}的前n项和Tn .
, 求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】极坐标与直角坐标系xOy有相同的长度单位,以原点O为极点,以x轴正半轴为极轴.曲线C1的极坐标方程为ρ﹣2cosθ=0,曲线C1的参数方程为![]() (t是参数,m是常数)
(t是参数,m是常数)
(Ⅰ)求C1的直角坐标方程和C2的普通方程;
(Ⅱ)若C2与C1有两个不同的公共点,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,a∈R.
,a∈R.
(1)求函数f(x)的单调区间;
(2)若函数f(x)有两个零点x1 , x2 , (x1<x2),求证:1<x1<a<x2<a2 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com