
分析 设三个正根为x1,x2,x3;从而可得a>0,b=-a(x1+x2+x3),c=a(x1x2+x3x2+x1x3),d=-ax1x2x3,从而利用分析法证明即可.
解答 证明:设三个正根为x1,x2,x3;
则φ(x)=ax3+bx2+cx+d
=a(x-x1)(x-x2)(x-x3)
=a(x3-(x1+x2+x3)x2+(x1x2+x3x2+x1x3)x-x1x2x3),
∵φ(0)<0,∴a>0;
b=-a(x1+x2+x3),c=a(x1x2+x3x2+x1x3),d=-ax1x2x3,
要证2b3+9a2d-7abc≤0,
只要证-2a3(x1+x2+x3)-9a3x1x2x3+7a3(x1+x2+x3)(x1x2+x3x2+x1x3)≤0,
只要证-2(x1+x2+x3)-9x1x2x3+7(x1+x2+x3)(x1x2+x3x2+x1x3)≤0,
只要证-2(x1+x2+x3)+7(x1+x2+x3)(x1x2+x3x2+x1x3)≤9x1x2x3,
只要证2x13+2x23+2x33≥x1x22+x3x22+x12x2+x32x2+x12x3+x1x32,
∵x13+x23-x1x22-x12x2=(x1-x2)2(x1+x2)≥0,
∴x13+x23≥x1x22+x12x2,
同理可得,x13+x33≥x1x32+x12x3,
x23+x33≥x2x32+x22x3,
∴2x13+2x23+2x33≥x1x22+x3x22+x12x2+x32x2+x12x3+x1x32,
∴原不等式成立.
点评 本题考查了根与系数的关系应用及分析法的应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-1≤x<5} | B. | {x|1<x<5} | C. | {x|1≤x<5} | D. | {x|-1≤x≤1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≠2且m≠3 | B. | m≠2,m≠3且m≠0 | C. | m=3 | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽豪州蒙城县一中高二上月考一数学试卷(解析版) 题型:选择题
一个等比数列的前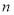 项和为45,前
项和为45,前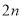 项和为60,则前
项和为60,则前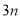 项和为( )
项和为( )
A.85 B.108 C.73 D.65
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com