
【题目】已知直线![]() 的方程为
的方程为![]() ,抛物线
,抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,点
,点![]() 是抛物线
是抛物线![]() 上到直线
上到直线![]() 距离最小的点.
距离最小的点.
(1)求点![]() 的坐标;
的坐标;
(2)若直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,
两点,![]() 为
为![]() 中点,且
中点,且![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)(1,2) (2)9x+3y-7=0
【解析】
(1)根据点到直线的距离公式和二次函数的性质得出P点坐标;(2)设出点M的坐标,由向量坐标化得到M(1,-![]() ),设出点A和点B的坐标,代入抛物线,两式做差得到斜率,由点斜式得到直线方程.
),设出点A和点B的坐标,代入抛物线,两式做差得到斜率,由点斜式得到直线方程.
(1)设点P的坐标为(x0,y0),则y02=4x0,所以,点P到直线的距离:
d =![]() =
=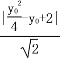 =
=![]() =
=![]() ≥
≥![]()
当且仅当y0=2时取最小值,此时P点坐标为(1,2).
(2)设点M的坐标为(x1,y1)因为![]() =3
=3![]() , 又点P(1,2),又F(1,0)可得:(0,-2)=3(x1-1,y1-0)
, 又点P(1,2),又F(1,0)可得:(0,-2)=3(x1-1,y1-0)
经计算得:点M(1,-![]() )
)
设点A(x2,y2)点B(x3,y3),于是![]()
两式相减可得:(y3- y2)( y3+y2)=4(x3-x2) 化简得:![]() =
=![]() ,
,
所以k=-3
于是,y+![]() =-3(x-1),整理得9x+3y-7=0
=-3(x-1),整理得9x+3y-7=0


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,离心率为
,离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
, ![]() .
.
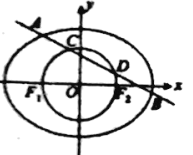
(1)求椭圆的方程;
(2)若直线![]() :
: ![]() 与椭圆交于
与椭圆交于![]() ,
, ![]() 两点,与以
两点,与以![]() 为直径的圆交于
为直径的圆交于![]() ,
, ![]() 两点,且满足
两点,且满足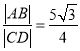 ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由国家公安部提出,国家质量监督检验检疫总局发布的《车辆驾驶人员血液、呼气酒精含量阀值与检验标准(![]() )》于
)》于![]() 年
年![]() 月
月![]() 日正式实施.车辆驾驶人员酒饮后或者醉酒后驾车血液中的酒精含量阀值见表.经过反复试验,一般情况下,某人喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”见图,
日正式实施.车辆驾驶人员酒饮后或者醉酒后驾车血液中的酒精含量阀值见表.经过反复试验,一般情况下,某人喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”见图,

喝![]() 瓶啤酒的情况
瓶啤酒的情况
且图表示的函数模型 ,则该人喝一瓶啤酒后至少经过多长时间才可以驾车(时间以整小时计算)?(参考数据:
,则该人喝一瓶啤酒后至少经过多长时间才可以驾车(时间以整小时计算)?(参考数据:![]() ,
,![]() )
)
( )
驾驶行为类型 | 阀值 |
饮酒后驾车 |
|
醉酒后驾车 |
|
车辆驾车人员血液酒精含量阀值
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲同学写出三个不等式:![]() :
:![]() ,
,![]() :
:![]() ,
,![]() :
:![]() ,然后将
,然后将![]() 的值告诉了乙、丙、丁三位同学,要求他们各用一句话来描述,以下是甲、乙、丙、丁四位同学的描述:
的值告诉了乙、丙、丁三位同学,要求他们各用一句话来描述,以下是甲、乙、丙、丁四位同学的描述:
乙:![]() 为整数;
为整数;
丙:![]() 是
是![]() 成立的充分不必要条件;
成立的充分不必要条件;
丁:![]() 是
是![]() 成立的必要不充分条件;
成立的必要不充分条件;
甲:三位同学说得都对,则![]() 的值为__________.
的值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() >0)的部分图象如图所示,A,B分别是这部分图象上的最高点、最低点,
>0)的部分图象如图所示,A,B分别是这部分图象上的最高点、最低点,![]() 为坐标原点,若
为坐标原点,若![]() ·
·![]() =0,
=0,![]() 则下列结论:①函数
则下列结论:①函数![]() 是周期为4的奇函数;②函数
是周期为4的奇函数;②函数![]() 是周期为4的偶函数;③函数
是周期为4的偶函数;③函数![]() 的最大值是
的最大值是![]() ;④函数
;④函数![]() 向左平移
向左平移![]() 个单位后得到的函数图象关于原点对称;其中错误命题的个数是( )
个单位后得到的函数图象关于原点对称;其中错误命题的个数是( )
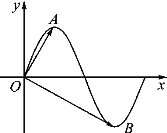
A.3B.2C.1D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点A(m, ![]() )(m∈R且m>0)为圆心的圆与x轴相交于O,B两点,与y轴相交于O,C两点,其中O为坐标原点.
)(m∈R且m>0)为圆心的圆与x轴相交于O,B两点,与y轴相交于O,C两点,其中O为坐标原点.
(1)当m=2时,求圆A的标准方程;
(2)当m变化时,△OBC的面积是否为定值?若是,请求出该定值;若不是,请说明理由;
(3)设直线![]() 与圆A相交于P,Q两点,且 |OP|=|OQ|,求 |PQ| 的值.
与圆A相交于P,Q两点,且 |OP|=|OQ|,求 |PQ| 的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,离心率为
,离心率为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() 的周长为8.
的周长为8.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com