
【题目】已知一元二次方程x2+(1+a)x+a+b+1=0的两个实根为x1,x2,且0<x1<1,x2>1,则 ![]() 的取值范围是( )
的取值范围是( )
A.(-2,- ![]() )
)
B.(-1,- ![]() )
)
C.(-2, ![]() )
)
D.(-1, ![]() )
)
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】一个正方体的平面展开图及该正方体的直观图的示意图如图所示.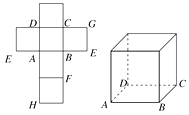
(1)请按字母F、G、H标记在正方体相应地顶点处(不需要说明理由);
(2)判断平面BEG与平面ACH的位置关系.并说明你的结论;
(3)证明:直线DF⊥平面BEG.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从装有 2个红球和 2个白球的口袋中任取 2个球,则下列每对事件中,互斥事件的对数是( )对
(1)“至少有 1个白球”与“都是白球” (2)“至少有 1个白球”与“至少有 1个红球”
(3)“至少有 1个白球”与“恰有 2个白球” (4)“至少有 1个白球”与“都是红球”
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设公差大于0的等差数列{ ![]() }的前n项和为
}的前n项和为 ![]() .已知
.已知 ![]() ,且
,且 ![]() ,
, ![]() ,
, ![]() 成等比数列.记数列
成等比数列.记数列 ![]() 的前n项和为
的前n项和为 ![]() .
.
(1)求 ![]() ;
;
(2)若对于任意的n ![]() ,k
,k ![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京101中学校园内有一个“少年湖”,湖的两侧有一个音乐教室和一个图书馆,如图,若设音乐教室在A处,图书馆在B处,为测量A,B两地之间的距离,某同学选定了与A,B不共线的C处,构成△ABC,以下是测量的数据的不同方案:①测量∠A,AC,BC;②测量∠A,∠B,BC;③测量∠C,AC,BC;④测量∠A,∠C,∠B. 其中一定能唯一确定A,B两地之间的距离的所有方案的序号是_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三棱锥P﹣ABC中,△ABC是边长为3的等边三角形,D是线段AB的中点,DE∩PB=E,且DE⊥AB,若∠EDC=120°,PA= ![]() ,PB=
,PB= ![]() ,则三棱锥P﹣ABC的外接球的表面积为 .
,则三棱锥P﹣ABC的外接球的表面积为 . 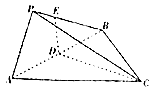
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的中心在原点,焦点在
的中心在原点,焦点在 ![]() 轴上,长轴长为4,且点
轴上,长轴长为4,且点 ![]() 在椭圆
在椭圆 ![]() 上.
上.
(1)求椭圆 ![]() 的方程;
的方程;
(2)设 ![]() 是椭圆
是椭圆 ![]() 长轴上的一个动点,过
长轴上的一个动点,过 ![]() 作斜率为
作斜率为 ![]() 的直线
的直线 ![]() 交椭圆
交椭圆 ![]() 于
于 ![]() 、
、 ![]() 两点,求证:
两点,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题 ![]() ,命题方程
,命题方程 ![]() 表示焦点在
表示焦点在 ![]() 轴上的双曲线.
轴上的双曲线.
(1)命题 ![]() 为真命题,求实数
为真命题,求实数 ![]() 的取值范围;
的取值范围;
(2)若命题“ ![]() ”为真,命题“
”为真,命题“ ![]() ”为假,求实数
”为假,求实数 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com