
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形,![]() 为
为![]() 的中点,
的中点,![]() 平面
平面![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,
,![]()

(1)证明:![]() 平面
平面![]() ;
;
(2)如果二面角![]() 的正切值为2,求
的正切值为2,求![]() 的值.
的值.
【答案】(1)祥见解析;(2)a=2.
【解析】
试题(1)由PO⊥平面ABCD,得PO⊥AD,由∠ADC=45°,AD=AC,得AD⊥AC,从而证明AD⊥平面PAC.(2)法一,先利用三垂线定理作出二面角M-AC-D的平面角:连结DO,作MG⊥DO于G,作GH⊥AO于H,因为M是PD中点,且MG⊥DO,所以G为DO中点,且MG⊥平面ABCD,显然,∠MHG即为二面角M-AC-D的平面角.然后在直角三角形MHG中,可用a表示出的正切值,从而由已知即可求出a的值;法二,以OA为x轴,OP为y轴,O为坐标原点建立空间直角坐标系,利用空间向量知亦可求.
试题解析: (1)证明:由题意,∠ADC=45o,AD=AC =1,故∠DAC=90o
即DA⊥AC.又因为 PO⊥平面ABCD,
所以,DA⊥PO,DA⊥平面PAC 4分
(2)法一:连结DO,作MG⊥DO于G,作GH⊥AO于H,因为M是PD中点,且MG⊥DO,所以G为DO中点,且MG⊥平面ABCD,显然,∠MHG即为二面角M-AC-D的平面角. 8分
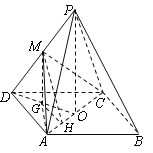
因为GH⊥AO,且G为DO中点,所以![]() ,而
,而![]() ,故
,故![]() ,PO="2MG=2." 12分
,PO="2MG=2." 12分
法二:建立如图所示的空间直角坐标系O-xyz,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
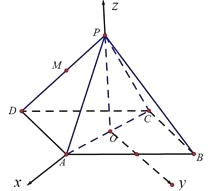
设平面MAC的法向量为![]() ,
,![]() ,
,![]() ,则
,则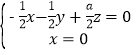 ,所以
,所以![]() 的一个取值为
的一个取值为
![]() 10分
10分
平面ACD的法向量为![]() .
.
设二面角的平面角为![]() ,
,
因为![]() ,所以
,所以![]()
a=2 12分


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】在万众创新的大经济背景下,某成都青年面包店推出一款新面包,每个面包的成本价为![]() 元,售价为
元,售价为![]() 元,该款面包当天只出一炉(一炉至少
元,该款面包当天只出一炉(一炉至少![]() 个,至多
个,至多![]() 个),当天如果没有售完,剩余的面包以每个
个),当天如果没有售完,剩余的面包以每个![]() 元的价格处理掉,为了确定这一炉面包的个数,该店记录了这款新面包最近
元的价格处理掉,为了确定这一炉面包的个数,该店记录了这款新面包最近![]() 天的日需求量(单位:个),整理得下表:
天的日需求量(单位:个),整理得下表:
日需求量 |
|
|
|
|
|
频数 |
|
|
|
|
|
(1)根据表中数据可知,频数![]() 与日需求量
与日需求量![]() (单位:个)线性相关,求
(单位:个)线性相关,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)以![]() 天记录的各日需求量的频率代替各日需求量的概率,若该店这款新面包出炉的个数为
天记录的各日需求量的频率代替各日需求量的概率,若该店这款新面包出炉的个数为![]() ,记当日这款新面包获得的总利润为
,记当日这款新面包获得的总利润为![]() (单位:元).求
(单位:元).求![]() 的分布列及其数学期望.
的分布列及其数学期望.
相关公式: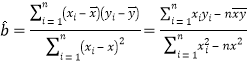 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:①直线![]() 的斜率
的斜率![]() ,则直线
,则直线![]() 的倾斜角
的倾斜角![]() ;②直线
;②直线![]() :
:![]() 与以
与以![]() 、
、![]() 两点为端点的线段相交,则
两点为端点的线段相交,则![]() 或
或![]() ;③如果实数
;③如果实数![]() 满足方程
满足方程![]() ,那么
,那么![]() 的最大值为
的最大值为![]() ;④直线
;④直线![]() 与椭圆
与椭圆![]() 恒有公共点,则
恒有公共点,则![]() 的取值范围是
的取值范围是![]() .其中正确命题的序号是______
.其中正确命题的序号是______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂销售部以箱为单位销售某种零件,每箱的定价为200元,低于100箱按原价销售;不低于100箱通过双方议价,买方能以优惠![]() 成交的概率为0.6,以优惠
成交的概率为0.6,以优惠![]() 成交的概率为0.4.
成交的概率为0.4.
(1)甲、乙两单位都要在该厂购买150箱这种零件,两单位各自达成的成交价相互独立,求甲单位优惠比例不低于乙单位优惠比例的概率;
(2)某单位需要这种零件650箱,求购买总价![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱![]() 中,AB=3,
中,AB=3,![]() =4,M为
=4,M为![]() 的中点,P是BC边上的一点,且由点P沿棱柱侧面经过棱
的中点,P是BC边上的一点,且由点P沿棱柱侧面经过棱![]() 到M点的最短路线长为
到M点的最短路线长为![]() ,设这条最短路线与
,设这条最短路线与![]() 的交点为N,求
的交点为N,求
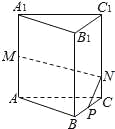
(1)该三棱柱的侧面展开图的对角线长.
(2)PC和NC的长
(3)平面NMP与平面ABC所成二面角(锐角)的大小(用反三角函数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将边长分别为![]() 的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第1个、第2个、……、第
的正方形叠放在一起,形成如图所示的图形,由小到大,依次记各阴影部分所在的图形为第1个、第2个、……、第![]() 个阴影部分图形.设前
个阴影部分图形.设前![]() 个阴影部分图形的面积的平均值为
个阴影部分图形的面积的平均值为![]() .记数列
.记数列![]() 满足:
满足: .
.

(1)求![]() 的表达式及数列
的表达式及数列![]() 的通项公式;
的通项公式;
(2)记![]()
![]() 若
若![]() ,其中
,其中![]() 为常数,且
为常数,且![]()
 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其中一个焦点F在直线
,其中一个焦点F在直线![]() 上.
上.
(1)求椭圆C的方程;
(2)若直线![]() 和直线
和直线![]() 与椭圆分别相交于点
与椭圆分别相交于点![]() 、
、![]() 、
、![]() 、
、![]() ,求
,求![]() 的值;
的值;
(3)若直线![]() 与椭圆交于P,Q两点,试求
与椭圆交于P,Q两点,试求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=aln x+![]() (a∈R).
(a∈R).
(1)当a=1时,求f(x)在x∈[1,+∞)内的最小值;
(2)若f(x)存在单调递减区间,求a的取值范围;
(3)求证ln(n+1)>![]() (n∈N*).
(n∈N*).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com