已知a,b都是实数,则“a+b≥4”是“a2+b2≥4”的( )
A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
【答案】
分析:由于a+b≥4,,则(a+b)
2≥16,而a
2+b
2≥2ab,则a
2+b
2≥8>4;令a=b=
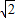
,满足a
2+b
2≥4,而此时a+b=2

<4.故“a+b≥4”是“a
2+b
2≥4”的充分而不必要条件.
解答:解:由于a+b≥4,则(a+b)
2≥16,即a
2+b
2+2ab≥16,而a
2+b
2≥2ab,则2(a
2+b
2)≥a
2+b
2+2ab≥16,所以a
2+b
2≥8>4;
由于a
2+b
2≥4,a,b都是实数,若a=b=
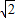
,而此时a+b=2

<4.故“a+b≥4”是“a
2+b
2≥4”的充分而不必要条件.
故答案选A.
点评:判断充要条件的方法是:
①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;
②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;
③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;
④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.
⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.

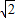 ,满足a2+b2≥4,而此时a+b=2
,满足a2+b2≥4,而此时a+b=2 <4.故“a+b≥4”是“a2+b2≥4”的充分而不必要条件.
<4.故“a+b≥4”是“a2+b2≥4”的充分而不必要条件.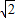 ,而此时a+b=2
,而此时a+b=2 <4.故“a+b≥4”是“a2+b2≥4”的充分而不必要条件.
<4.故“a+b≥4”是“a2+b2≥4”的充分而不必要条件.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案