
【题目】已知三棱锥![]() (如图一)的平面展开图(如图二)中,四边形
(如图一)的平面展开图(如图二)中,四边形![]() 为边长等于
为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形,在三棱锥
均为正三角形,在三棱锥![]() 中:
中:
(I)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若点![]() 在棱
在棱![]() 上运动,当直线
上运动,当直线![]() 与平面
与平面![]() 所成的角最大时,求二面角
所成的角最大时,求二面角![]() 的余弦值.
的余弦值.
图一
图二
【答案】(1)见解析(2)![]()
【解析】
(1)设AC的中点为O,证明PO垂直AC,OB,结合平面与平面垂直判定,即可.(2)建立直角坐标系,分别计算两相交平面的法向量,结合向量的数量积公式,计算夹角,即可.
(Ⅰ)设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() .
.
由题意,得![]() ,
,
![]() ,
,![]() .
.
因为在![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,
的中点,
所以![]() ,
,
因为在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() ,所以
,所以![]() .
.
因为![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
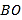
(Ⅱ)由(Ⅰ)知,![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 是直线
是直线![]() 与平面
与平面![]() 所成的角,
所成的角,
且![]() ,
,
所以当![]() 最短时,即
最短时,即![]() 是
是![]() 的中点时,
的中点时,![]() 最大.
最大.
由![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,于是以
,于是以
![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图示空间直角坐标系,
轴建立如图示空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则
由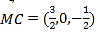 得:
得:![]() .
.
令![]() ,得
,得![]() ,
,![]() ,即
,即![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由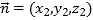 得:
得:![]() ,
,
令![]() ,得
,得![]() ,
,![]() ,即
,即![]() .
.
![]() .
.
由图可知,二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】当前全世界人民越来越关注环境保护问题,某地某监测站点于2018年8月起连续n天监测空气质量指数(AQI),数据统计如下表:
空气质量指数(μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] |
空气质量等级 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 |
天数 | 20 | 40 | m | 10 | 5 |
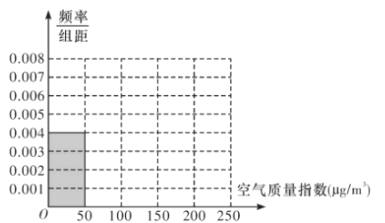
(1)根据所给统计表和频率分布直方图中的信息求出n,m的值,并完成频率分布直方图;
(2)由频率分布直方图,求该组数据的平均数与中位数;
(3)在空气质量指数分别为[0,50]和(50,100]的监测数据中,用分层抽样的方法抽取6天,从中任意选取2天,求事件A“两天空气质量等级都为良”发生的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济全球化、信息化的发展,企业之间的竞争从资源的争夺转向人才的竞争.吸引、留住培养和用好人才成为人力资源管理的战略目标和紧迫任务.在此背景下,某信息网站在15个城市中对刚毕业的大学生的月平均收入薪资和月平均期望薪资做了调查,数据如图所示.
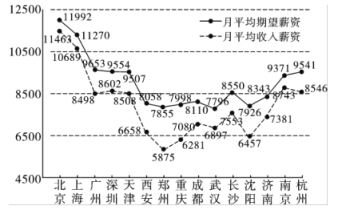
(1)若某大学毕业生从这15座城市中随机选择一座城市就业,求该生选中月平均收人薪资高于8000元的城市的概率;
(2)若从月平均收入薪资与月平均期望薪资之差高于1000元的城市中随机选择2座城市,求这2座城市的月平均期望薪资都高于8000元或都低于8000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的四个顶点组成的四边形的面积为
的四个顶点组成的四边形的面积为![]() ,且经过点
,且经过点 .
.

(1)求椭圆![]() 的方程;
的方程;
(2)若椭圆![]() 的下顶点为
的下顶点为![]() ,如图所示,点
,如图所示,点![]() 为直线
为直线![]() 上的一个动点,过椭圆
上的一个动点,过椭圆![]() 的右焦点
的右焦点![]() 的直线
的直线![]() 垂直于
垂直于![]() ,且与
,且与![]() 交于
交于![]() 两点,与
两点,与![]() 交于点
交于点![]() ,四边形
,四边形![]() 和
和![]() 的面积分别为
的面积分别为![]() .求
.求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (
(![]() 为参数)曲线C2的参数方程为
为参数)曲线C2的参数方程为![]() (
(![]() ,
,![]() 为参数)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=
为参数)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=![]() 与C1,C2各有一个交点.当
与C1,C2各有一个交点.当![]() =0时,这两个交点间的距离为2,当
=0时,这两个交点间的距离为2,当![]() =
=![]() 时,这两个交点重合.
时,这两个交点重合.
(1)分别说明C1,C2是什么曲线,并求出a与b的值;
(2)设当![]() =
=![]() 时,l与C1,C2的交点分别为A1,B1,当
时,l与C1,C2的交点分别为A1,B1,当![]() =-
=-![]() 时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标平面中,已知点![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,其中
,其中![]() 是正整数,对平面上任一点
是正整数,对平面上任一点![]() ,记
,记![]() 为
为![]() 关于点
关于点![]() 的对称点,
的对称点,![]() 为
为![]() 关于点
关于点![]() 的对称点,…,
的对称点,…,![]() 为
为![]() 关于点
关于点![]() 的对称点.
的对称点.
(1)求向量![]() 的坐标;
的坐标;
(2)当点![]() 在曲线
在曲线![]() 上移动时,点
上移动时,点![]() 的轨迹是函数
的轨迹是函数![]() 的图像,其中
的图像,其中![]() 是以3为周期的周期函数,且当
是以3为周期的周期函数,且当![]() 时,
时,![]() .求以曲线
.求以曲线![]() 为图像的函数在
为图像的函数在![]() 上的解析式;
上的解析式;
(3)对任意偶数![]() ,用
,用![]() 表示向量
表示向量![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面四边形![]() 中,
中,![]() ,
,![]() 是
是![]() ,
,![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起至
折起至![]() ,使平面
,使平面![]() ,则四面体
,则四面体![]() 中,下列结论不正确的是( )
中,下列结论不正确的是( )
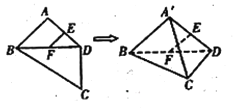
A.![]() 平面
平面![]()
B.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
C.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
D.直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com