
【题目】已知函数![]() ,直线
,直线![]() 为曲线
为曲线![]() 的切线(
的切线(![]() 为自然对数的底数).
为自然对数的底数).
(1)求实数![]() 的值;
的值;
(2)用![]() 表示
表示![]() 中的最小值,设函数
中的最小值,设函数![]() ,若函数
,若函数
![]() 为增函数,求实数
为增函数,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)先求导,然后利用导数等于![]() 求出切点的横坐标,代入两个曲线的方程,解方程组,可求得
求出切点的横坐标,代入两个曲线的方程,解方程组,可求得![]() ;(2)设
;(2)设![]() 与
与![]() 交点的横坐标为
交点的横坐标为![]() ,利用导数求得
,利用导数求得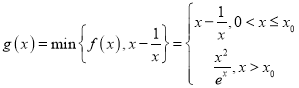 ,从而
,从而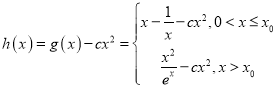 ,然后利用
,然后利用![]() 求得
求得![]() 的取值范围为
的取值范围为![]() .
.
试题解析:
(1)对![]() 求导得
求导得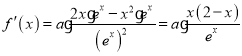 .....................1分
.....................1分
设直线![]() 与曲线
与曲线![]() 切于点
切于点![]() ,则
,则
 ,解得
,解得![]() ,
,
所以![]() 的值为1..........................................3分
的值为1..........................................3分
(2)记函数![]() ,下面考察函数
,下面考察函数![]() 的符号,
的符号,
对函数![]() 求导得
求导得![]() ......................4分
......................4分
当![]() 时,
时,![]() 恒成立.................................5分
恒成立.................................5分
当![]() 时,
时,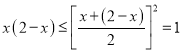 ,
,
从而![]() .....................7分
.....................7分
∴![]() 在
在![]() 上恒成立,故
上恒成立,故![]() 在
在![]() 上单调递减.
上单调递减.
![]() ,∴
,∴![]() ,
,
又曲线 ![]() 在
在![]() 上连续不间断,所以由函数的零点存在性定理及其单调性知
上连续不间断,所以由函数的零点存在性定理及其单调性知![]() 唯一的
唯一的![]() ,使
,使![]() .
.
∴![]() ;
;![]() ,
,![]() ,
,
∴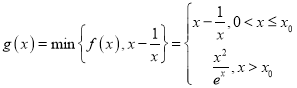 ,
,
从而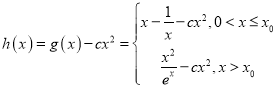 ,
,
∴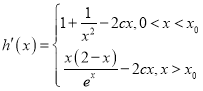 ,..........................9分
,..........................9分
由函数![]() 为增函数,且曲线
为增函数,且曲线![]() 在
在![]() 上连续不断知
上连续不断知![]() 在
在![]() ,
,![]() 上恒成立.
上恒成立.
①当![]() 时,
时,![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,
上恒成立,
记![]() ,则
,则![]() ,
,
当![]() 变化时,
变化时,![]() 变化情况列表如下:
变化情况列表如下:
|
| 3 |
|
|
| 0 |
|
|
| 极小值 |
|
∴![]() ,
,
故“![]() 在
在![]() 上恒成立”只需
上恒成立”只需![]() ,即
,即 ![]() .
.
②当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() 在
在![]() 上恒成立,
上恒成立,
综合①②知,当![]() 时,函数
时,函数![]() 为增函数.
为增函数.
故实数![]() 的取值范围是
的取值范围是![]() ...............................12分
...............................12分


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】六个面都是平行四边形的四棱柱称为平行六面体。如,在平行四边形 ABCD 中,有AC2+BD2=2(AB2+AD2) ,那么在图(2)的平行六面体 ABCD-A1B1C1D1 中有AC12+BD12+CA12+DB12 等于( ) 12
12
A.2(AB2+AD2+AA12)
B.3(AB2+AD2+AA12)
C.4(AB2+AD2+AA12)
D.3(AB2+AD2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定圆P:x2+y2=2x及抛物线S:y2=4x,过圆心P作直线l,此直线与上述两曲线的四个交点,自上而下顺次为A,B,C,D;如果线段AB,BC,CD的长度按此顺序构成一个等差数列,则直线l的方程为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且满足2![]() acsinB=
acsinB=![]() .
.
(1)求角C的大小:
(2)若bsin(π-A)=acosB,且b=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的中心在原点,焦点为![]() ,且离心率为
,且离心率为 ![]() .
.
(1)求椭圆的方程;
(2)直线(与坐标轴 不平行)与椭圆交于不同的两点,且线段中点的横坐标为![]() ,求直线倾斜角的取值范围.
,求直线倾斜角的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lg(x2﹣3x)的定义域为集合A,函数 ![]() 的定义域为集合B(其中a∈R,且a>0).
的定义域为集合B(其中a∈R,且a>0).
(1)当a=1时,求集合B;
(2)若A∩B≠,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三个内角分别为A,B,C,且A≠ ![]() .
.
(1)化简 ![]() ;
;
(2)若角A满足sinA+cosA= ![]() .
.
(i)试判断△ABC是锐角三角形还是钝角三角形,并说明理由;
(ii)求tanA的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+bx2+cx的极值点为x=﹣ ![]() 和x=1
和x=1
(1)求b,c的值与f(x)的单调区间
(2)当x∈[﹣1,2]时,不等式f(x)<m恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com