
【题目】在△ABC中,三个内角是A,B,C的对边分别是a,b,c,其中c=10,且 ![]() .
.
(1)求证:△ABC是直角三角形;
(2)设圆O过A,B,C三点,点P位于劣弧AC上,∠PAB=60°,求四边形ABCP的面积.
【答案】
(1)证明:根据正弦定理得, ![]() .
.
整理为:sinAcosA=sinBcosB,即sin2A=sin2B,
因为0<A<π,0<B<π,所以0<2A<2π,0<2B<2π,所以A=B,或者A+B= ![]() .
.
由于 ![]() ,
,
故△ABC是直角三角形.
(2)解:由(1)可得:a=6,b=8.
在Rt△ABC中,sin∠CAB= ![]() =
= ![]() ,cos∠CAB=
,cos∠CAB= ![]()
sin∠PAC=sin(60°﹣∠CAB)
=sin60°cos∠CAB﹣cos60°sin∠CAB
= ![]() .
.
连接PB,在Rt△APB中,AP=ABcos∠PAB=5.
所以四边形ABCP的面积
S四边形△ABCP=S△ABC+S△PAC
= ![]()
= ![]() .
.
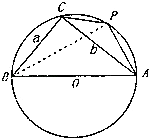
【解析】(1)由题设条件 ![]() .利用正弦定理可得
.利用正弦定理可得 ![]() ,整理得讨论知,A=B或者A+B=
,整理得讨论知,A=B或者A+B= ![]() .又
.又 ![]() ,所以A+B=
,所以A+B= ![]() . 由此可以得出,△ABC是直角三角形;(2)将四边形ABCP的面积表示成两个三角形S△ABC与S△PAC的和,S△ABC易求,S△PAC需求出线段PA的长度与sin∠PAC的值,利用三角形的面积公式求解即可.
. 由此可以得出,△ABC是直角三角形;(2)将四边形ABCP的面积表示成两个三角形S△ABC与S△PAC的和,S△ABC易求,S△PAC需求出线段PA的长度与sin∠PAC的值,利用三角形的面积公式求解即可.
【考点精析】根据题目的已知条件,利用正弦定理的定义的相关知识可以得到问题的答案,需要掌握正弦定理:![]() .
.


科目:高中数学 来源: 题型:
【题目】设Sn为正项数列{an}的前n项和,a1=2,Sn+1(Sn+1﹣2Sn+1)=3Sn(Sn+1),则a100等于( )
A.2×398
B.4×398
C.2×399
D.4×399
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}中,已知a1=1,a4=8,若a3 , a5分别为等差数列{bn}的第4项和第16项.
(1)求数列{an}﹑{bn}的通项公式;
(2)令cn=anbn , 求数列{cn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图在四面体OABC中,OA,OB,OC两两垂直,且OB=OC=3,OA=4,给出如下判断: ①存在点D(O点除外),使得四面体DABC有三个面是直角三角形;
②存在点D,使得点O在四面体DABC外接球的球面上;
③存在唯一的点D使得OD⊥平面ABC;
④存在点D,使得四面体DABC是正棱锥;
⑤存在无数个点D,使得AD与BC垂直且相等.
其中正确命题的序号是(把你认为正确命题的序号填上).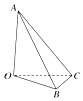
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣3x2+a(6﹣a)x+c.
(1)当c=19时,解关于a的不等式f(1)>0;
(2)若关于x的不等式f(x)>0的解集是(﹣1,3),求实数a,c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,离心率为 ![]() ,短轴长为4
,短轴长为4 ![]() . (Ⅰ)求椭圆C的标准方程;
. (Ⅰ)求椭圆C的标准方程;
(Ⅱ)直线x=2与椭圆C交于P、Q两点,A、B是椭圆O上位于直线PQ两侧的动点,且直线AB的斜率为 ![]() .
.
①求四边形APBQ面积的最大值;
②设直线PA的斜率为k1 , 直线PB的斜率为k2 , 判断k1+k2的值是否为常数,并说明理由.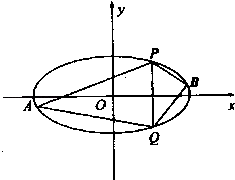
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,点A1在平面ABC内的射影O为AC的中点,A1O=2,AB⊥BC,AB=BC= ![]() 点P在线段A1B上,且cos∠PAO=
点P在线段A1B上,且cos∠PAO= ![]() ,则直线AP与平面A1AC所成角的正弦值为 .
,则直线AP与平面A1AC所成角的正弦值为 . 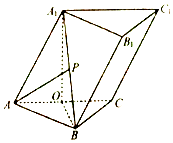
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知m,n,s,t∈R+ , m+n=2, ![]() +
+ ![]() =9,其中m,n是常数,当s+t取最小值
=9,其中m,n是常数,当s+t取最小值 ![]() 时,m,n对应的点(m,n)是椭圆
时,m,n对应的点(m,n)是椭圆 ![]() =1的一条弦的中点,则此弦所在的直线方程 .
=1的一条弦的中点,则此弦所在的直线方程 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com