
【题目】已知椭圆 ![]() 的焦距为
的焦距为![]() ,斜率为
,斜率为![]() 的直线与椭圆交于
的直线与椭圆交于![]() 两点,若线段
两点,若线段![]() 的中点为
的中点为![]() ,且直线
,且直线![]() 的斜率为
的斜率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若过左焦点![]() 斜率为
斜率为![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]()
![]() 为椭圆上一点,且满足
为椭圆上一点,且满足![]() ,问:
,问:![]() 是否为定值?若是,求出此定值,若不是,说明理由.
是否为定值?若是,求出此定值,若不是,说明理由.
【答案】(1) ![]() .
.
(2) ![]() 为定值
为定值![]() .过程见解析.
.过程见解析.
【解析】分析:(1)焦距说明![]() ,用点差法可得
,用点差法可得![]() =
=![]() .这样可解得
.这样可解得![]() ,得椭圆方程;
,得椭圆方程;
(2)若![]() ,这种特殊情形可直接求得
,这种特殊情形可直接求得![]() ,在
,在![]() 时,直线
时,直线![]() 方程为
方程为![]() ,设
,设![]() ,把直线方程代入椭圆方程,后可得
,把直线方程代入椭圆方程,后可得![]() ,然后由纺长公式计算出弦长
,然后由纺长公式计算出弦长![]() ,同时直线
,同时直线![]() 方程为
方程为![]() ,代入椭圆方程可得
,代入椭圆方程可得![]() 点坐标,从而计算出
点坐标,从而计算出![]() ,最后计算
,最后计算![]() 即可.
即可.
详解:(1)由题意可知![]() ,设
,设![]() ,代入椭圆可得:
,代入椭圆可得:
![]() ,两式相减并整理可得,
,两式相减并整理可得,
![]() ,即
,即![]() .
.
又因为![]() ,
,![]() ,代入上式可得,
,代入上式可得,![]() .
.
又![]() ,所以
,所以![]() ,
,
故椭圆的方程为![]() .
.
(2)由题意可知,![]() ,当
,当![]() 为长轴时,
为长轴时,![]() 为短半轴,此时
为短半轴,此时
![]() ;
;
否则,可设直线![]() 的方程为
的方程为![]() ,联立
,联立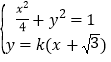 ,消
,消![]() 可得,
可得,
![]() ,
,
则有:![]() ,
,
所以![]()
设直线![]() 方程为
方程为![]() ,联立
,联立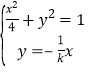 ,根据对称性,
,根据对称性,
不妨得![]() ,
,
所以![]() .
.
故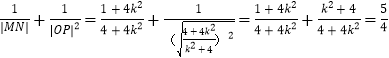 ,
,
综上所述,![]() 为定值
为定值![]() .
.


科目:高中数学 来源: 题型:
【题目】“克拉茨猜想”又称“![]() 猜想”,是德国数学家洛萨克拉茨在1950年世界数学家大会上公布的一个猜想:任给一个正整数
猜想”,是德国数学家洛萨克拉茨在1950年世界数学家大会上公布的一个猜想:任给一个正整数![]() ,如果
,如果![]() 是偶数,就将它减半;如果
是偶数,就将它减半;如果![]() 为奇数就将它乘3加1,不断重复这样的运算,经过有限步后,最终都能够得到1.己知正整数
为奇数就将它乘3加1,不断重复这样的运算,经过有限步后,最终都能够得到1.己知正整数![]() 经过6次运算后得到1,则
经过6次运算后得到1,则![]() 的值为__________.
的值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地西红柿从2月1号起开始上市,通过市场调查,得到西红柿种植成本![]() (单位:元/100
(单位:元/100![]() )与上市时间
)与上市时间![]() (距2月1日的天数,单位:天)的数据如下表:
(距2月1日的天数,单位:天)的数据如下表:
时间 | 50 | 110 | 250 |
成本 | 150 | 108 | 150 |
(1)根据上表数据,从下列函数中选取一个函数描述西红柿种植成本![]() 与上市时间
与上市时间![]() 的变化关系:
的变化关系:![]() ;
;
(2)利用(1)中选取的函数,求西红柿种植成本![]() 最低时的上市天数
最低时的上市天数![]() 及最低种植成本.
及最低种植成本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在区间![]() 上的函数y=f(x)的图象关于直线x=-
上的函数y=f(x)的图象关于直线x=-![]() 对称,当x∈
对称,当x∈![]() 时,函数f(x)=Asin(ωx+φ)
时,函数f(x)=Asin(ωx+φ)![]() 的图象如图所示.
的图象如图所示.

(1)求函数y=f(x)在![]() 上的表达式;
上的表达式;
(2)求方程f(x)=![]() 的解.
的解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
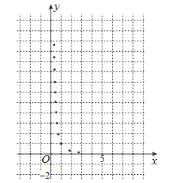
|
|
|
|
|
|
|
1.47 | 20.6 | 0.78 | 2.35 | 0.81 | -19.3 | 16.2 |
表中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若旋转的弧度数![]() 与单位时间内煤气输出量
与单位时间内煤气输出量![]() 成正比,那么
成正比,那么![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为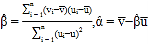 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求证:![]()
(2)若函数![]() 的图象与直线
的图象与直线![]() 没有交点,求实数
没有交点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() ,则是否存在实数
,则是否存在实数![]() ,使得
,使得![]() 的最小值为
的最小值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某盒子中共有![]() 个小球,编号为
个小球,编号为![]() 号至
号至![]() 号,其中有
号,其中有![]() 个红球、
个红球、![]() 个黄球和
个黄球和![]() 个绿球,这些球除颜色和编号外完全相同.
个绿球,这些球除颜色和编号外完全相同.
(1)若从盒中一次随机取出![]() 个球,求取出的
个球,求取出的![]() 个球中恰有
个球中恰有![]() 个颜色相同的概率;
个颜色相同的概率;
(2)若从盒中逐一取球,每次取后立即放回,共取![]() 次,求恰有
次,求恰有![]() 次取到黄球的概率;
次取到黄球的概率;
(3)若从盒中逐一取球,每次取后不放回,记取完黄球所需次数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运输公司接受了向抗洪救灾地区每天送至少![]() 支援物资的任务.该公司有
支援物资的任务.该公司有![]() 辆载重
辆载重![]() 的
的![]() 型卡车与
型卡车与![]() 辆载重为
辆载重为![]() 的
的![]() 型卡车,有
型卡车,有![]() 名驾驶员,每辆卡车每天往返的次数为
名驾驶员,每辆卡车每天往返的次数为![]() 型卡车
型卡车![]() 次,
次,![]() 型卡车
型卡车![]() 次;每辆卡车每天往返的成本费
次;每辆卡车每天往返的成本费![]() 型为
型为![]() 元,
元,![]() 型为
型为![]() 元.请为公司安排一下,应如何调配车辆,才能使公司所花的成本费最低?若只安排
元.请为公司安排一下,应如何调配车辆,才能使公司所花的成本费最低?若只安排![]() 型或
型或![]() 型卡车,所花的成本费分别是多少?
型卡车,所花的成本费分别是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com