
分析 (1)由Sn=an+1+n2-3,n∈N*,结合S3=15,可得a3,进一步求得a2和a1的值;
(2)由(1)猜测归纳出an=2n+1,然后直接利用数学归纳法证明.
解答 解:(1)∵S3=S2+a3=(a3+1)+a3=2a3+1,
又S3=15,∴a3=7,
∵S2=a3+1=8,
又S2=S1+a2=(a2-2)+a2=2a2-2,
∴a2=5,a1=S1=a2-2=3,
综上知a1=3,a2=5,a3=7;
(2)由(1)猜想an=2n+1,
下面用数学归纳法证明.
①当n=1时,a1=3,2×1+1=3结论成立;
②假设当n=k(k≥1)时,结论成立,即ak=2k+1,
则${S_k}=3+5+7+…+(2k+1)=\frac{3+(2k+1)}{2}×k=k(k+2)$,
又${S_k}={a_{k+1}}+{k^2}-3$,∴$k(k+2)={a_{k+1}}+{k^2}-3$,解得ak+1=2k+3,
∴ak+1=2(k+1)+1,即当n=k+1时,结论成立;
综①②所述,对任意n∈N*,an=2n+1.
点评 本题考查数列递推式,考查了利用数学归纳法证明与自然数有关的命题,属中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
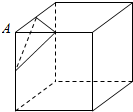 如图,设A是棱长为2的正方体的一个顶点,过从顶点A出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,截去8个三棱锥,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:
如图,设A是棱长为2的正方体的一个顶点,过从顶点A出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,截去8个三棱锥,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{y^2}{3}-\frac{x^2}{12}=1$ | B. | $\frac{x^2}{3}-\frac{y^2}{12}=1$ | C. | $\frac{y^2}{2}-\frac{x^2}{8}=1$ | D. | $\frac{x^2}{2}-\frac{y^2}{8}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>0} | B. | {x|0<x<2} | C. | {x|x≥2} | D. | {x|x>2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
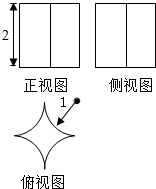 已知某几何体的三视图如图所示,其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆,则该几何体的表面积为( )
已知某几何体的三视图如图所示,其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆,则该几何体的表面积为( )| A. | 8-π | B. | 8+π | C. | 8-2π | D. | 8+2π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3\sqrt{2}$ | B. | $4\sqrt{2}$ | C. | $5\sqrt{2}$ | D. | $5\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com