
【题目】在椭圆![]() 上任取一点
上任取一点![]() (
(![]() 不为长轴端点),连结
不为长轴端点),连结![]() 、
、![]() ,并延长与椭圆
,并延长与椭圆![]() 分别交于点
分别交于点![]() 、
、![]() 两点,已知
两点,已知![]() 的周长为8,
的周长为8,![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设坐标原点为![]() ,当
,当![]() 不是椭圆的顶点时,直线
不是椭圆的顶点时,直线![]() 和直线
和直线![]() 的斜率之积是否为定值?若是定值,请求出这个定值;若不是定值,请说明理由.
的斜率之积是否为定值?若是定值,请求出这个定值;若不是定值,请说明理由.
【答案】(1)![]() ;(2)是定值,值为
;(2)是定值,值为![]() .
.
【解析】
(1)根据椭圆的定义,结合![]() 的周长为8,求出
的周长为8,求出![]() 的值,设出点
的值,设出点![]() 的坐标,结合三角形面积公式,椭圆的范围,
的坐标,结合三角形面积公式,椭圆的范围,![]() 面积的最大值为
面积的最大值为![]() .可以求出
.可以求出![]() 的关系,进而求出
的关系,进而求出![]() 的值,最后求出椭圆
的值,最后求出椭圆![]() 的方程;
的方程;
(2)设出直线![]() 的方程与椭圆方程联立,利用解方程组,求出
的方程与椭圆方程联立,利用解方程组,求出![]() 点坐标,同理求出
点坐标,同理求出![]() 的坐标,最后通过斜率公式,计算出直线
的坐标,最后通过斜率公式,计算出直线![]() 和直线
和直线![]() 的斜率之积是定值.
的斜率之积是定值.
(1)因为![]() 的周长为8,所以有
的周长为8,所以有![]()
设![]() ,因为
,因为![]() 面积的最大值为
面积的最大值为![]() .所以
.所以![]() 的最大值为
的最大值为![]() ,由椭圆的范围,当
,由椭圆的范围,当![]() 时,面积最大,因此有
时,面积最大,因此有![]() ,而
,而![]() ,因为
,因为![]() ,所以
,所以![]() ,所以椭圆标准方程为:
,所以椭圆标准方程为:![]() ;
;
(2)当![]() 不是椭圆的顶点时,因此
不是椭圆的顶点时,因此![]() .
.
直线![]() 的方程为:
的方程为:![]() ,与椭圆的方程联立,得:
,与椭圆的方程联立,得:
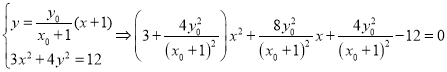 ,
,
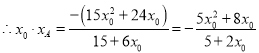 ,
,![]() ,
,
同理直线![]() 的方程为:
的方程为:![]() ,与椭圆的方程联立,得:
,与椭圆的方程联立,得:
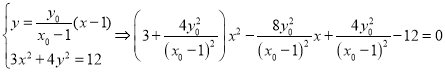
![]()
![]() ,
,
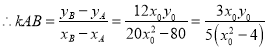 ,
,
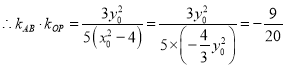 为定值.
为定值.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:
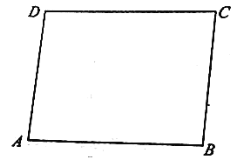
【题目】如图,矩形![]() 是某生态农庄的一块植物栽培基地的平面图,现欲修一条笔直的小路
是某生态农庄的一块植物栽培基地的平面图,现欲修一条笔直的小路![]() (宽度不计)经过该矩形区域,其中
(宽度不计)经过该矩形区域,其中![]() 都在矩形
都在矩形![]() 的边界上.已知
的边界上.已知![]() ,
,![]() (单位:百米),小路
(单位:百米),小路![]() 将矩形
将矩形![]() 分成面积分别为
分成面积分别为![]() ,
,![]() (单位:平方百米)的两部分,其中
(单位:平方百米)的两部分,其中![]() ,且点
,且点![]() 在面积为
在面积为![]() 的区域内,记小路
的区域内,记小路![]() 的长为
的长为![]() 百米.
百米.
(1)若![]() ,求
,求![]() 的最大值;
的最大值;
(2)若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年上半年我国多个省市暴发了“非洲猪瘟”疫情,生猪大量病死,存栏量急剧下降,一时间猪肉价格暴涨,其他肉类价格也跟着大幅上扬,严重影响了居民的生活.为了解决这个问题,我国政府一方面鼓励有条件的企业和散户防控疫情,扩大生产;另一方面积极向多个国家开放猪肉进口,扩大肉源,确保市场供给稳定.某大型生猪生产企业分析当前市场形势,决定响应政府号召,扩大生产决策层调阅了该企业过去生产相关数据,就“一天中一头猪的平均成本与生猪存栏数量之间的关系”进行研究.现相关数据统计如下表:
生猪存栏数量 | 2 | 3 | 4 | 5 | 8 |
头猪每天平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.5 |
(1)研究员甲根据以上数据认为![]() 与
与![]() 具有线性回归关系,请帮他求出
具有线性回归关系,请帮他求出![]() 关于
关于![]() 的线.性回归方程
的线.性回归方程![]() (保留小数点后两位有效数字)
(保留小数点后两位有效数字)
(2)研究员乙根据以上数据得出![]() 与
与![]() 的回归模型:
的回归模型:![]() .为了评价两种模型的拟合效果,请完成以下任务:
.为了评价两种模型的拟合效果,请完成以下任务:
①完成下表(计算结果精确到0.01元)(备注:![]() 称为相应于点
称为相应于点![]() 的残差);
的残差);
生猪存栏数量 | 2 | 3 | 4 | 5 | 8 | |
头猪每天平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.5 | |
模型甲 | 估计值 | |||||
残差 | ||||||
模型乙 | 估计值 | 3.2 | 2.4 | 2 | 1.76 | 1.4 |
残差 | 0 | 0 | 0 | 0.14 | 0.1 | |
②分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() 的大小,判断哪个模型拟合效果更好.
的大小,判断哪个模型拟合效果更好.
(3)根据市场调查,生猪存栏数量达到1万头时,饲养一头猪每一天的平均收入为7.5元;生猪存栏数量达到1.2万头时,饲养一头猪每一天的平均收入为7.2元若按(2)中拟合效果较好的模型计算一天中一头猪的平均成本,问该生猪存栏数量选择1万头还是1.2万头能获得更多利润?请说明理由.(利润=收入-成本)
参考公式: .
.
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查中学生每天玩游戏的时间是否与性别有关,随机抽取了男、女学生各50人进行调查,根据其日均玩游戏的时间绘制了如下的频率分布直方图.

(1)求所调查学生日均玩游戏时间在![]() 分钟的人数;
分钟的人数;
(2)将日均玩游戏时间不低于60分钟的学生称为“游戏迷”,已知“游戏迷”中女生有6人;
①根据已知条件,完成下面的![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“游戏迷”和性别关系;
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“游戏迷”和性别关系;
非游戏迷 | 游戏迷 | 合计 | |
男 | |||
女 | |||
合计 |
②在所抽取的“游戏迷”中按照分层抽样的方法抽取10人,再在这10人中任取9人进行心理干预,求这9人中男生全被抽中的概率.
附: (其中
(其中![]() 为样本容量).
为样本容量).
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的两个顶点
的两个顶点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,且
,且![]() 所在直线的斜率之积等于
所在直线的斜率之积等于![]() ,记顶点
,记顶点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求顶点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,点
两点,点![]() 在曲线
在曲线![]() 上,且
上,且![]() 为
为![]() 的重心(
的重心(![]() 为坐标原点),求证:
为坐标原点),求证:![]() 的面积为定值,并求出该定值.
的面积为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 是常数,且
是常数,且![]() ),曲线
),曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 的值;
的值;
(2)若存在![]() (其中
(其中![]() 是自然对数的底),使得
是自然对数的底),使得![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,均存在
,均存在![]() ,使得方程
,使得方程![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为等差数列,
为等差数列,![]() 为等比数列,公比为
为等比数列,公比为![]() .令
.令![]() .
.
(1)若![]() .
.
①当![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
②设![]() ,
,![]() ,试比较
,试比较![]() 与
与![]() 的大小?并证明你的结论.
的大小?并证明你的结论.
(2)问集合![]() 中最多有多少个元素?并证明你的结论.
中最多有多少个元素?并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为3的正方形ABCD中,点E,F分别在边AB,BC上(如图1),且BE=BF,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于点A′(如图2).

(1)求证:A′D⊥EF;
(2)BF![]() BC时,求点A′到平面DEF的距离.
BC时,求点A′到平面DEF的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com