
【题目】甲、乙两高射炮同时向一架敌机射击,已知甲击中敌机的概率是0.6,乙击中敌机的概率为0.5,求敌机被击中的概率.
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为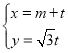 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和C的直角坐标方程;
的普通方程和C的直角坐标方程;
(2)直线![]() 上的点
上的点![]() 为曲线
为曲线![]() 内的点,且直线
内的点,且直线![]() 与曲线
与曲线![]() 交于
交于![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为等边三角形,
为等边三角形,![]() ,P,Q依次为AC,AB上的点,且线段PQ将
,P,Q依次为AC,AB上的点,且线段PQ将![]() 分为面积相等的两部分,设
分为面积相等的两部分,设![]() ,
,![]() ,
,![]() .
.
(1)用解析式将t表示成x的函数;
(2)用解析式将y表示成x的函数;
(3)求y的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市现有人口总数为![]() 万人,如果年自然增长率为
万人,如果年自然增长率为![]() ,试解答下列问题:
,试解答下列问题:
(1)写出该城市经过![]() 年后的人口总数关于
年后的人口总数关于![]() 的函数关系式;
的函数关系式;
(2)用程序流程图表示计算![]() 年以后该城市人口总数的算法;
年以后该城市人口总数的算法;
(3)用程序流程图表示如下算法:计算大约多少年以后该城市人口将达到![]() 万人.
万人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司招聘员工,指定三门考试课程,有两种考试方案.方案一:考试三门课程,至少有两门及格为考试通过;方案二:在三门课程中,随机选取两门,这两门都及格为考试通过.假设某应聘者对三门指定课程考试及格的概率分别是![]() ,
,![]() ,
,![]() ,且三门课程考试是否及格相互之间没有影响.
,且三门课程考试是否及格相互之间没有影响.
(1)分别求该应聘者用方案一和方案二时考试通过的概率;
(2)试比较该应聘者在上述两种方案下考试通过的概率的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,边
,边![]() 上一点
上一点![]() ,这里
,这里![]() 异于
异于![]() .由
.由![]() 引边
引边![]() 的垂线
的垂线![]() 是垂足,再由
是垂足,再由![]() 引边
引边![]() 的垂线
的垂线![]() 是垂足,又由
是垂足,又由![]() 引边
引边![]() 的垂线
的垂线![]() 是垂足.同样的操作连续进行,得到点
是垂足.同样的操作连续进行,得到点![]() ,
,![]() ,
,![]() .设
.设![]() ,如图所示.
,如图所示.

(1)求![]() 的值;
的值;
(2)某同学对上述已知条件的研究发现如下结论:![]() ,问该同学这个结论是否正确并说明理由;
,问该同学这个结论是否正确并说明理由;
(3)用![]() 和
和![]() 表示
表示![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】著名数学家华罗庚先生曾说过:“数缺形时少直观,形缺数时难入微数形结合百般好,隔裂分家万事休.”在数学的学习和研究中,我们经常用函数的图象来研究函数的性质,也经常用函数的解析式来琢磨函数的图象的特征,如某体育品牌的LOGO为![]() ,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
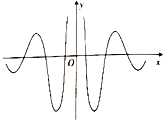
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图像是由函数
的图像是由函数![]() 的图像经如下变换得到:先将
的图像经如下变换得到:先将![]() 图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移
图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移![]() 个单位长度.
个单位长度.
(Ⅰ)求函数![]() 的解析式,并求其图像的对称轴方程;
的解析式,并求其图像的对称轴方程;
(Ⅱ)已知关于![]() 的方程
的方程![]() 在
在![]() 内有两个不同的解
内有两个不同的解![]() .
.
(1)求实数m的取值范围;
(2)证明:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
按照某学者的理论,假设一个人生产某产品单件成本为![]() 元,如果他卖出该产品的单价为
元,如果他卖出该产品的单价为![]() 元,则他的满意度为
元,则他的满意度为![]() ;如果他买进该产品的单价为
;如果他买进该产品的单价为![]() 元,则他的满意度为
元,则他的满意度为![]() .如果一个人对两种交易(卖出或买进)的满意度分别为
.如果一个人对两种交易(卖出或买进)的满意度分别为![]() 和
和![]() ,则他对这两种交易的综合满意度为
,则他对这两种交易的综合满意度为![]() .
.
现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为![]() 元和
元和![]() 元,甲买进A与卖出B的综合满意度为
元,甲买进A与卖出B的综合满意度为![]() ,乙卖出A与买进B的综合满意度为
,乙卖出A与买进B的综合满意度为![]()
(1)求![]() 和
和![]() 关于
关于![]() 、
、![]() 的表达式;当
的表达式;当![]() 时,求证:
时,求证:![]() =
=![]() ;
;
(2)设![]() ,当
,当![]() 、
、![]() 分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?(3)记(2)中最大的综合满意度为
分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?(3)记(2)中最大的综合满意度为![]() ,试问能否适当选取
,试问能否适当选取![]() 、
、![]() 的值,使得
的值,使得![]() 和
和![]() 同时成立,但等号不同时成立?试说明理由。
同时成立,但等号不同时成立?试说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com