
���� ��1����x=��cos�ȣ�y=��sin�ȣ�x2+y2=��2���ɵ�����C����ͨ���̣����ô��뷨���ɵ�ֱ��l����ͨ���̣�
��2����ֱ��l�IJ������̴������ߵ���ͨ���̣������б�ʽ����0��Τ�ﶨ������ϲ����ļ������壬�ⷽ�̣����ɵõ�����m��ֵ��
��� �⣺��1����x=��cos�ȣ�y=��sin�ȣ�x2+y2=��2��
����C�ļ����귽���Ǧ�=2cos�ȣ���Ϊ��2=2��cos�ȣ�
����x2+y2=2x����Բ��x-1��2+y2=1��
Ӵֱ��l�IJ���������$\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{2}t+m}\\{y=\frac{1}{2}t}\end{array}\right.$��tΪ��������
�ɵ�x-$\sqrt{3}$y-m=0��
��2����$\left\{\begin{array}{l}{x=\frac{\sqrt{3}}{2}t+m}\\{y=\frac{1}{2}t}\end{array}\right.$����Բ��x-1��2+y2=1��
�ɵ�t2+$\sqrt{3}$��m-1��t+m2-m=0��
�ɡ�=3��m-1��2-4��m2-m����0���ɵ�-1��m��3��
��mΪ�Ǹ������ɵ�0��m��3��
��t1��t2�Ƿ��̵��������ɵ�t1t2=m2-m��
|PA|•|PB|=1���ɵ�|m2-m|=1��
���m=1��1��$\sqrt{2}$��
��0��m��3���ɵ�m=1��1+$\sqrt{2}$��
���� ���⿼�鼫����ϵ���̡��������̺�ֱ�����귽�̵Ļ���������ֱ�߲������̵����ã���Ҫ�Dz����ļ������壬���黯�����������������������е��⣮


 �·Ƿ��̸����100��ϵ�д�
�·Ƿ��̸����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{364}$ | B�� | $\frac{1}{121}$ | C�� | $\frac{120}{121}$ | D�� | $\frac{363}{364}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
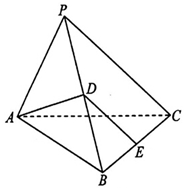 ������P-ABC�У�AP=AB��ƽ��PAB��ƽ��ABC����ABC=90�㣬D��E�ֱ�ΪPB��BC���е㣮
������P-ABC�У�AP=AB��ƽ��PAB��ƽ��ABC����ABC=90�㣬D��E�ֱ�ΪPB��BC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
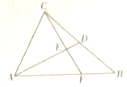 ��ͼ��ABC����D��BC�е㣬$\overrightarrow{AF}$=2$\overrightarrow{FB}$��CF��AD���ڵ�E����$\overrightarrow{AD}$=a��$\overrightarrow{AB}$=b��
��ͼ��ABC����D��BC�е㣬$\overrightarrow{AF}$=2$\overrightarrow{FB}$��CF��AD���ڵ�E����$\overrightarrow{AD}$=a��$\overrightarrow{AB}$=b���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{2}$ | B�� | �� | C�� | 2�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com