
【题目】已知函数![]() (其中
(其中![]() 为常数).
为常数).
(1)若![]() 在
在![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 在
在![]() 上的最大值为
上的最大值为![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)对函数进行求导,再利用参变分离,将问题转化为恒成立问题;
(2)对函数进行求导得![]() ,再对
,再对![]() 分成三种情况,即
分成三种情况,即![]() 、
、![]() 、
、![]() 进行分类讨论,分别求出最大值,进而得到
进行分类讨论,分别求出最大值,进而得到![]() 的值.
的值.
(1)由![]() 可得
可得![]() ,
,
由![]() 在
在![]() 上单调递增可得
上单调递增可得![]() 在
在![]() 上恒成立,
上恒成立,
即![]() ,
,![]()
![]() ,由
,由![]() 可得
可得![]() ,
,
故只需![]() ,
,![]()
![]() ,即实数
,即实数![]() 的取值范围是
的取值范围是![]() .
.
(2)由(1)可知![]() ,
,
①当![]() ,即
,即![]() 时,
时,![]() 在(1,2)上恒成立,
在(1,2)上恒成立,
故![]() 在(1,2)上单调递增,则
在(1,2)上单调递增,则![]() 在[1,2]上的最大值为
在[1,2]上的最大值为![]() ,
,
故![]() ,满足
,满足![]() ;
;
②当![]() ,即
,即![]() 时,
时,![]() 在(1,2)上恒成立,
在(1,2)上恒成立,
故![]() 在(1,2)上单调递减,则
在(1,2)上单调递减,则![]() 在[1,2]上的最大值为
在[1,2]上的最大值为![]() ,
,
故![]() ,不满足
,不满足![]() ,舍去;
,舍去;
③当![]() ,即
,即![]() 时,由
时,由![]() 可得
可得![]() .
.
![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
即![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
故![]() 的最大值为
的最大值为![]() ,即
,即![]() ,
,
所以,![]() ,不满足
,不满足![]() ,舍去.
,舍去.
综上可知,![]() .
.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的极坐标方程;
的极坐标方程;
(2)将曲线![]() 上所有点的横坐标不变,纵坐标缩短到原来的
上所有点的横坐标不变,纵坐标缩短到原来的![]() 倍,得到曲线
倍,得到曲线![]() ,若
,若![]() 与
与![]() 的交点为
的交点为![]() (异于坐标原点
(异于坐标原点![]() ),
),![]() 与
与![]() 的交点为
的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若在两个成语中,一个成语的末字恰是另一成语的首字,则称这两个成语有顶真关系,现从分别贴有成语“人定胜天”、“争先恐后”、“一马当先”、“天马行空”、“先发制人”的5张大小形状完全相同卡片中,任意抽取2张,则这2张卡片上的成语有顶真关系的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为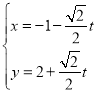 (其中
(其中![]() 为参数),以原点为极点,以
为参数),以原点为极点,以![]() 轴为极轴建立极坐标系,曲线
轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 为常数,且
为常数,且![]() ),直线
),直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)若![]() ,求实数
,求实数![]() 的值;
的值;
(2)若点![]() 的直角坐标为
的直角坐标为![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年5月20日以来,广东自西北到东南出现了一次明显降雨.为了对某地的降雨情况进行统计,气象部门对当地20日~28日9天记录了其中100小时的降雨情况,得到每小时降雨情况的频率分布直方图如下:

若根据往年防汛经验,每小时降雨量在![]() 时,要保持二级警戒,每小时降雨量在
时,要保持二级警戒,每小时降雨量在![]() 时,要保持一级警戒.
时,要保持一级警戒.
(1)若从记录的这100小时中按照警戒级别采用分层抽样的方法抽取10小时进行深度分析.
①求一级警戒和二级警戒各抽取多少小时;
②若从这10个小时中任选2个小时,则这2个小时中恰好有1小时属于一级警戒的概率.(2)若以每组的中点代表该组数据值,求这100小时内的平均降雨量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为
的左焦点为![]() ,椭圆上动点
,椭圆上动点![]() 到点
到点![]() 的最远距离和最近距离分别为
的最远距离和最近距离分别为![]() 和
和![]() .
.
(1)求椭圆的方程;
(2)设![]() 分别为椭圆的左、右顶点,过点
分别为椭圆的左、右顶点,过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 、
、![]() 两点,若
两点,若![]() ,
,![]() 为坐标原点,求
为坐标原点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三共有1000位学生,为了分析某次的数学考试成绩,采取随机抽样的方法抽取了50位高三学生的成绩进行统计分析,得到如图所示频数分布表:
分组 |
|
|
|
|
|
频数 | 3 | 11 | 18 | 12 | 6 |
(1)根据频数分布表计算成绩在![]() 的频率并计算这组数据的平均值
的频率并计算这组数据的平均值![]() (同组的数据用该组区间的中点值代替);
(同组的数据用该组区间的中点值代替);
(2)用分层抽样的方法从成绩在![]() 和
和![]() 的学生中共抽取5人,从这5人中任取2人,求成绩在
的学生中共抽取5人,从这5人中任取2人,求成绩在![]() 和
和![]() 中各有1人的概率.
中各有1人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩,其中有三个数据模糊.
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
立定跳远(单位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
30秒跳绳(单位:次) | 63 | a | 75 | 60 | 63 | 72 | 70 | a1 | b | 65 |
在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则
(A)2号学生进入30秒跳绳决赛
(B)5号学生进入30秒跳绳决赛
(C)8号学生进入30秒跳绳决赛
(D)9号学生进入30秒跳绳决赛
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com