
本题满分14分)
设函数 .
.
(1)若 ,求函数
,求函数 的极值;
的极值;
(2)若 ,试确定
,试确定 的单调性;
的单调性;
(3)记 ,且
,且 在
在 上的最大值为M,证明:
上的最大值为M,证明: .
.
解:(1)若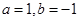 ,则
,则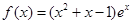
有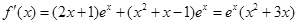
令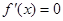 得
得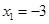 ,
, -------------------------------------------1分
-------------------------------------------1分
∵当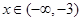 时
时 ,当
,当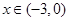 时
时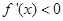 ,当
,当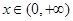 时,
时,
∴当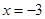 时,函数
时,函数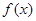 有极大值,
有极大值,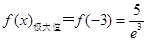 ,-----------------------------2分
,-----------------------------2分
当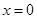 时,函数
时,函数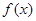 有极小值,
有极小值,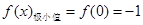 --------------------------------3分
--------------------------------3分
(2)∵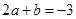 即
即 
又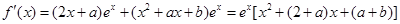
∴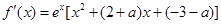 =
=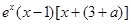 --------------------------------5分
--------------------------------5分
当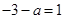 即
即 时,
时,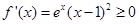
∴函数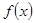 在
在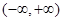 上单调递增;--------------------------------------------------------------6分
上单调递增;--------------------------------------------------------------6分
当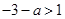 ,即
,即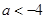 时,由
时,由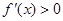 得
得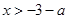 或
或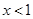 ,
,
由 得
得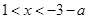 ;------------------------------------------------------------------------7分
;------------------------------------------------------------------------7分
当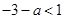 ,即
,即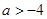 时,由
时,由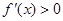 得
得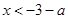 或
或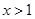 ,
,
由 得
得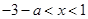 ;------------------------------------------------------------------------8分
;------------------------------------------------------------------------8分
综上得:当 时,函数
时,函数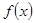 在
在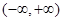 上单调递增;
上单调递增;
当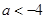 时,函数
时,函数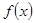 在
在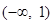 和
和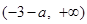 上单调递增,在
上单调递增,在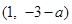 上单调递减-9分
上单调递减-9分
当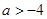 时,函数
时,函数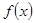 在
在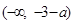 和
和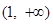 上单调递增,在
上单调递增,在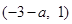 上单调递减.---10分
上单调递减.---10分
(3)根据题意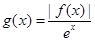 =
=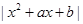 ,
,
∵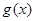 在
在 上的最大值为M,
上的最大值为M,
∴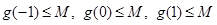
即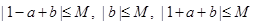 --------------------------------------12分
--------------------------------------12分
2=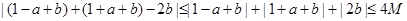
∴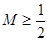 ---------------------------------------------14分
---------------------------------------------14分
【解析】略


科目:高中数学 来源: 题型:
(本题满分14分)
设函数![]() ,
,![]() 。
。
(1)若![]() ,过两点
,过两点![]() 和
和![]() 的中点作
的中点作![]() 轴的垂线交曲线
轴的垂线交曲线![]() 于点
于点![]() ,求证:曲线
,求证:曲线![]() 在点
在点![]() 处的切线
处的切线![]() 过点
过点![]() ;
;
(2)若![]() ,当
,当![]() 时
时![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2011——2012学年湖北省洪湖二中高三八月份月考试卷理科数学 题型:解答题
(本题满分14分)设椭圆 的左、右焦点分别为F1与
的左、右焦点分别为F1与
F2,直线 过椭圆的一个焦点F2且与椭圆交于P、Q两点,若
过椭圆的一个焦点F2且与椭圆交于P、Q两点,若 的周长为
的周长为 。
。
(1)求椭圆C的方程;
(2)设椭圆C经过伸缩变换 变成曲线
变成曲线 ,直线
,直线 与曲线
与曲线 相切
相切
且与椭圆C交于不同的两点A、B,若 ,求
,求 面积的取值范围。(O为坐标原点)
面积的取值范围。(O为坐标原点)
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省杭州市高三寒假作业数学卷三 题型:解答题
(本题满分14分)设M是由满足下列条件的函数 构成的集合:“①方
构成的集合:“①方 有实数根;②函数
有实数根;②函数 的导数
的导数 满足
满足 ”
”
(I)证明:函数 是集合M中的元素;
是集合M中的元素;
(II)证明:函数 具有下面的性质:对于任意
具有下面的性质:对于任意
 ,都存在
,都存在 ,使得等式
,使得等式 成立。
成立。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省揭阳市高三调研检测数学理卷 题型:解答题
本题满分14分)
设函数 .
.
(1)若 ,求函数
,求函数 的极值;
的极值;
(2)若 ,试确定
,试确定 的单调性;
的单调性;
(3)记 ,且
,且 在
在 上的最大值为M,证明:
上的最大值为M,证明: .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com