
【题目】已知函数f(x)满足f(x+y)=f(x)+f(y),当x>0时,有![]() ,且f(1)=﹣2
,且f(1)=﹣2
(1)求f(0)及f(﹣1)的值;
(2)判断函数f(x)的单调性,并利用定义加以证明;
(3)求解不等式f(2x)﹣f(x2+3x)<4.
【答案】(1)0,2(2)减函数(3)(﹣2,1).
【解析】试题分析:(1)令x=y=0求f(0)=0;再令x=-y=1得f(0)=f(1)+f(-1);从而求解;(2)可判断函数f(x)是R上的减函数,利用定义证明;(3)由(2)知,f(2x)﹣f(x2+3x)<4可化为f(2x-x2-3x)<f(-2);从而得x2+x-2<0,从而解得
试题解析:(1)令x=y=0得,
f(0)=f(0)+f(0);
故f(0)=0;
令x=﹣y=1得,
f(0)=f(1)+f(﹣1);
故f(﹣1)=f(0)﹣f(1)=2; (3分)
(2)函数f(x)是R上的减函数,证明如下,
令x=﹣y得,f(0)=f(x)+f(﹣x);
故f(x)=﹣f(﹣x);
任取x1,x2∈R,且x1<x2,
则f(x1)﹣f(x2)=f(x1)+f(﹣x2)
=f(x1﹣x2)=﹣f(x2﹣x1),
故由f(x2﹣x1)<0知,﹣f(x2﹣x1)>0,
从而得f(x1)﹣f(x2)>0,
则函数f(x)是R上的减函数; (4分)
(3)由(2)知,
f(2x)﹣f(x2+3x)<4可化为
f(2x﹣x2﹣3x)<f(﹣2);
故x2+x﹣2<0,
解得,x∈(﹣2,1). (5分)


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知过点![]() 的直线
的直线![]() 的参数方程是
的参数方程是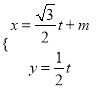 (
(![]() 为参数).以平面直角坐标系的原点为极点,
为参数).以平面直角坐标系的原点为极点, ![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程式为
的极坐标方程式为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解初三学生女生身高情况,某中学对初三女生身高进行了一次测量,所得数据整理后列出了频率分布表如下:
组 别 | 频数 | 频率 |
145.5~149.5 | 1 | 0.02 |
149.5~153.5 | 4 | 0.08 |
153.5~157.5 | 20 | 0.40 |
157.5~161.5 | 15 | 0.30 |
161.5~165.5 | 8 | 0.16 |
165.5~169.5 | m | n |
合 计 | M | N |
(1)求出表中![]() 所表示的数分别是多少?
所表示的数分别是多少?
(2)画出频率分布直方图.
(3)全体女生中身高在哪组范围内的人数最多?由直方图确定此组数据中位数是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.
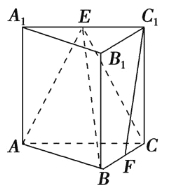
(1)求证:AB⊥平面B1BCC1; 平面ABE⊥平面B1BCC1;
(2)求证:C1F∥平面ABE;
(3)求三棱锥E-ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为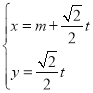 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,且曲线
,且曲线![]() 的左焦点
的左焦点![]() 在直线
在直线![]() 上.
上.
(1)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某渔场鱼群的最大养殖量为![]() 吨,为保证鱼群的生长空间,实际的养殖量
吨,为保证鱼群的生长空间,实际的养殖量![]() 要小于
要小于![]() ,留出适当的空闲量,空闲量与最大养殖量的比值叫空闲率,已知鱼群的年增加量
,留出适当的空闲量,空闲量与最大养殖量的比值叫空闲率,已知鱼群的年增加量![]() (吨)和实际养殖量
(吨)和实际养殖量![]() (吨)与空闲率的乘积成正比(设比例系数
(吨)与空闲率的乘积成正比(设比例系数![]() ).
).
(1)写出![]() 与
与![]() 的函数关系式,并指出定义域;
的函数关系式,并指出定义域;
(2)求鱼群年增长量的最大值;
(3)当鱼群年增长量达到最大值时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产A,B两种产品,生产1吨A种产品需要煤4吨、电18千瓦;生产1吨B种产品需要煤1吨、电15千瓦。现因条件限制,该企业仅有煤10吨,并且供电局只能供电66千瓦,若生产1吨A种产品的利润为10000元;生产1吨B种产品的利润是5000元,试问该企业如何安排生产,才能获得最大利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com