
【题目】已知数列{an}满足a1=1,an+1=3an+1.
(1)证明{an+ ![]() }是等比数列,并求{an}的通项公式;
}是等比数列,并求{an}的通项公式;
(2)证明: ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() .
.
【答案】
(1)证明: 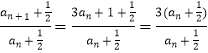 =3,
=3,
∵ ![]() ≠0,
≠0,
∴数列{an+ ![]() }是以首项为
}是以首项为 ![]() ,公比为3的等比数列;
,公比为3的等比数列;
∴an+ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() ;
;
(2)证明:由(1)知 ![]() ,
,
当n≥2时,∵3n﹣1>3n﹣3n﹣1,∴ ![]() <
< ![]() =
= ![]() ,
,
∴当n=1时, ![]() 成立,
成立,
当n≥2时, ![]() +
+ ![]() +…+
+…+ ![]() <1+
<1+ ![]() …+
…+ ![]() =
= ![]() =
= ![]() <
< ![]() .
.
∴对n∈N+时, ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() .
.
【解析】(1)根据等比数列的定义,后一项与前一项的比是常数,即 ![]() =常数,又首项不为0,所以为等比数列;再根据等比数列的通项化式,求出{an}的通项公式;(2)将
=常数,又首项不为0,所以为等比数列;再根据等比数列的通项化式,求出{an}的通项公式;(2)将 ![]() 进行放大,即将分母缩小,使得构成一个等比数列,从而求和,证明不等式.
进行放大,即将分母缩小,使得构成一个等比数列,从而求和,证明不等式.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系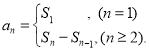 ),还要掌握等比数列的基本性质({an}为等比数列,则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列)的相关知识才是答题的关键.
),还要掌握等比数列的基本性质({an}为等比数列,则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列)的相关知识才是答题的关键.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣l|+|x﹣3|.
(1)解不等式f(x)≤6;
(2)若不等式f(x)≥ax﹣1对任意x∈R恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设ξ为随机变量,从侧面均是等边三角形的正四棱锥的8条棱中任选两条,ξ为这两条棱所成的角.
(1)求概率 ![]() ;
;
(2)求ξ的分布列,并求其数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面上,过点P作直线l的垂线所得的垂足称为点P在直线l上的投影,由区域  中的点在直线x+y﹣2=0上的投影构成的线段记为AB,则|AB|=( )
中的点在直线x+y﹣2=0上的投影构成的线段记为AB,则|AB|=( )
A.2 ![]()
B.4
C.3 ![]()
D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2acosB.
(1)证明:A=2B
(2)若△ABC的面积S= ![]() ,求角A的大小.
,求角A的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数x满足(x-a)(x-3a)<0,其中a>0,命题q:实数x满足(x-3)(x-2)≤0.
(1)若a=1,且p∧q为真,求实数x的取值范围.
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com