
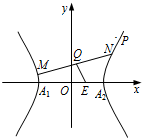
 如图所示,中心在原点,顶点A1、A2在x轴上,离心率为
如图所示,中心在原点,顶点A1、A2在x轴上,离心率为
| ||
| 3 |
| EQ |
| A2P |
| ||
| 3 |
| c |
| a |
| ||
| 3 |
| EQ |
| A2P |
| EQ |
| A2P |
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| a |
| ||
| 3 |
| 4 |
| 3 |
| 36 |
| a2 |
| 3×36 |
| 4a2 |
| x2 |
| 9 |
| y2 |
| 12 |
|
|
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
| 6k |
| 4-3k2 |
| x1+x2 |
| 2 |
| 3k |
| 4-3k2 |
| 4 |
| 4-3k2 |
| 3k |
| 4-3k2 |
| 4 |
| 4-3k2 |
| EQ |
| 3k |
| 4-3k2 |
| 4 |
| 4-3k2 |
| A2P |
| EQ |
| A2P |
| 3k |
| 4-3k2 |
| 4 |
| 4-3k2 |
| ||
| 3 |
| ||
| 3 |
| EQ |
| 2 |
| 3 |
| 2 |
| 3 |
| EQ |
| A2P |


科目:高中数学 来源: 题型:

(1)求飞船飞行的椭圆轨道的方程;
(2)飞船绕地球飞行了十四圈后,于16日5时59分返回舱与推进舱分离,结束巡天飞行,飞船共巡天飞行了约6×105 km,问飞船巡天飞行的平均速度是多少?(结果精确到1 km/s)(注:km/s即千米/秒)
查看答案和解析>>
科目:高中数学 来源: 题型:

(1)求飞船飞行的椭圆轨道的方程;
(2)飞船绕地球飞行了十四圈后,于16日5时59分返回舱与推进舱分离,结束巡天飞行,飞船共巡天飞行了约6×105 km,问飞船巡天飞行的平均速度是多少?(结果精确到1 km/s)(注:km/s即千米/秒)
查看答案和解析>>
科目:高中数学 来源:2010年江西省名校高考数学信息卷1(理科)(解析版) 题型:解答题
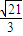 的双曲线C经过点P (6,6),动直线l经过点(0,1)与双曲线C交于M、N两点,Q为线段MN的中点.
的双曲线C经过点P (6,6),动直线l经过点(0,1)与双曲线C交于M、N两点,Q为线段MN的中点. =λ
=λ ,若存在,求λ值;若不存在,说明理由.
,若存在,求λ值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2010年江西省名校高考信息卷一(理) 题型:解答题
如图所示,中心在原点,顶点A1、A2在x轴上,离心率为的双曲线C经过点P (6 , 6),
动直线l经过点(0 , 1)与双曲线C交于M、N两点,Q为线段MN的中点.
 (1) 求双曲线C的标准方程;
(1) 求双曲线C的标准方程;
(2) 若E点为(1 , 0),是否存在实数λ使 =λ,若存在,
求λ值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com