
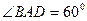 ,Q为AD的中点
,Q为AD的中点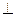 平面PAD
平面PAD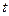 PC,试确定实数
PC,试确定实数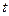 的值,使得PA//平面MQB
的值,使得PA//平面MQB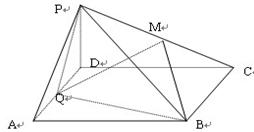
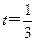 时, PA//平面MQB
时, PA//平面MQB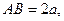 故
故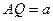 又
又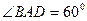
 =3
=3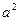
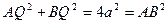
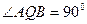 ,可知
,可知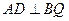 ,………………………………………2分
,………………………………………2分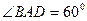 ,AD=AB,可知
,AD=AB,可知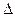 AB
AB D为等边三角形,又Q为AD的中点,所以也可证得
D为等边三角形,又Q为AD的中点,所以也可证得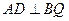 )
)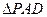

 中,PA="PD" ,Q为AD的中点
中,PA="PD" ,Q为AD的中点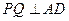 , …………………………………………………………………………3分
, …………………………………………………………………………3分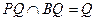

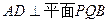 ………………………………………………………………4分
………………………………………………………………4分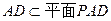 所以平面PQB
所以平面PQB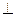 平面PAD………………………………6分
平面PAD………………………………6分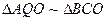 ∴
∴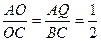 …
… …………………………………8分
…………………………………8分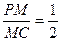 ,即
,即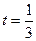 时,满足题意…………………………………………10分
时,满足题意…………………………………………10分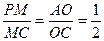


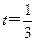 时, PA//平面MQB……………………………………………...12分
时, PA//平面MQB……………………………………………...12分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
 ,
, 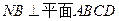 ,且MD=NB=1,E为BC 的中点 (1)求异面直线NE与AM所成角的余弦值
,且MD=NB=1,E为BC 的中点 (1)求异面直线NE与AM所成角的余弦值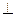 平面AMN,并求线段AS的长;
平面AMN,并求线段AS的长;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
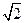 .
.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
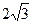 AF,且点M是线段EF的中点.
AF,且点M是线段EF的中点.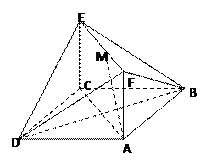
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com