
 .
.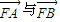 夹角为θ,且
夹角为θ,且 ,求直线m斜率的取值范围.
,求直线m斜率的取值范围.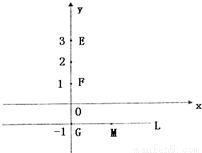
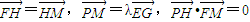 ,点P在直线x=a上,由抛物线定义,动点P的轨迹是以F为焦点,直线y=-1为准线的抛物线,求出动点P 轨迹方程;(Ⅱ)直线与抛物线相交,联立方程,利用伟大定理,寻找向量
,点P在直线x=a上,由抛物线定义,动点P的轨迹是以F为焦点,直线y=-1为准线的抛物线,求出动点P 轨迹方程;(Ⅱ)直线与抛物线相交,联立方程,利用伟大定理,寻找向量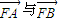 夹角为θ的余弦值,求出直线m斜率的取值范围.
夹角为θ的余弦值,求出直线m斜率的取值范围.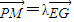 ,
, ,
,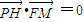 ,
,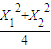
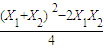 =4k2-6,y1y2
=4k2-6,y1y2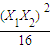 =9.
=9.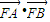 =(x1,y1-1)•(x2,y2-1)=x1x2+y1y2-(y1+y2)+1
=(x1,y1-1)•(x2,y2-1)=x1x2+y1y2-(y1+y2)+1 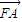 |•|
|•|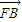 |=|FA1|•|FB1|=(y1+1)•(y2+1)=y1y2+(y1+y2)+1,
|=|FA1|•|FB1|=(y1+1)•(y2+1)=y1y2+(y1+y2)+1,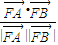 =
=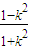 ≤cos
≤cos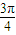 ≤-
≤- ,解得|k|≥1+
,解得|k|≥1+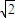
 ]∪[1+
]∪[1+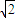 ,+∞)
,+∞)

科目:高中数学 来源: 题型:
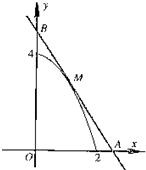 如图,已知M是函数y=4-x2(1<x<2)的图象C上一点,过M点作曲线C的切线与x轴、y轴分别交于点A,B,O是坐标原点,求△AOB面积的最小值.
如图,已知M是函数y=4-x2(1<x<2)的图象C上一点,过M点作曲线C的切线与x轴、y轴分别交于点A,B,O是坐标原点,求△AOB面积的最小值.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•九江一模)已知点G是△ABC的外心,
(2012•九江一模)已知点G是△ABC的外心,| GA |
| GB |
| GC |
| GA |
| AB |
| AC |
| 0 |
| GA |
| AB |
| OA |
查看答案和解析>>
科目:高中数学 来源: 题型:
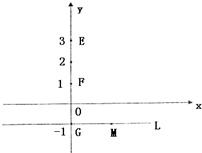 如图,O是坐标原点,已知三点E(0,3),F(0,1),G(0,-1),直线L:y=-1,M是直线L上的动点,H.P是坐标平面上的动点,且
如图,O是坐标原点,已知三点E(0,3),F(0,1),G(0,-1),直线L:y=-1,M是直线L上的动点,H.P是坐标平面上的动点,且| FH |
| HM |
| PM |
| EG |
| PH |
| FM |
| FA |
| FB |
| 3π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,O是坐标原点,已知三点E(0,3),F(0,1),G(0,-1),直线L:y=-1,M是直线L上的动点,H.P是坐标平面上的动点,且
如图,O是坐标原点,已知三点E(0,3),F(0,1),G(0,-1),直线L:y=-1,M是直线L上的动点,H.P是坐标平面上的动点,且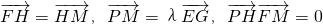 .
.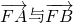 夹角为θ,且
夹角为θ,且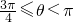 ,求直线m斜率的取值范围.
,求直线m斜率的取值范围.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com