
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知cosB= ![]() ,tanC=
,tanC= ![]() . (Ⅰ)求tanB和tanA;
. (Ⅰ)求tanB和tanA;
(Ⅱ)若c=1,求△ABC的面积.
【答案】解:(Ⅰ)在△ABC中,∵cosB= ![]() , ∴B为锐角,tanB=
, ∴B为锐角,tanB= ![]() ,
,
又tanC= ![]() ,tan(B+C)=
,tan(B+C)= ![]() =
= 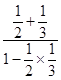 =1,
=1,
∴tanA=tan[180°﹣(B+C)]=﹣tan(B+C),
∴tanA=﹣1.
(Ⅱ)因0°<A<180°,由(Ⅰ)结论可得:A=135°,
∴在△ABC中,B,C均为锐角
∵cosB= ![]() ,tanC=
,tanC= ![]() ,
,
∴sinB= ![]() ,sinC=
,sinC= ![]() .
.
∴由 ![]() ,得a=
,得a= ![]() ,
,
故△ABC的面积为:S= ![]() acsinB=
acsinB= ![]()
【解析】(Ⅰ)由已知利用同角三角函数基本关系式可求tanB的值,利用两角和的正切函数公式可求tan(B+C),利用三角形内角和定理,诱导公式即可得解tanA的值.(Ⅱ)结合范围0°<A<180°,由(Ⅰ)可得A=135°,利用同角三角函数基本关系式可求cosB,sinB,sinC的值,利用正弦定理可求a,进而利用三角形面积公式即可计算得解.
【考点精析】根据题目的已知条件,利用两角和与差的正切公式和正弦定理的定义的相关知识可以得到问题的答案,需要掌握两角和与差的正切公式:![]() ;正弦定理:
;正弦定理:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】要得到函数y=sin(4x﹣ ![]() )的图象,只需将函数y=sin4x的图象( )
)的图象,只需将函数y=sin4x的图象( )
A.向左平移 ![]() 单位
单位
B.向右平移 ![]() 单位
单位
C.向左平移 ![]() 单位
单位
D.向右平移 ![]() 单位
单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知p:﹣x2+4x+12≥0,q:x2﹣2x+1﹣m2≤0(m>0).
(Ⅰ)若p是q充分不必要条件,求实数m的取值范围;
(Ⅱ)若“¬p”是“¬q”的充分条件,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时, ![]() .现已画出函数
.现已画出函数![]() 在
在![]() 轴左侧的图象,如图所示,请根据图象.
轴左侧的图象,如图所示,请根据图象.
(![]() )写出函数
)写出函数![]() 的增区间.
的增区间.
(![]() )写出函数
)写出函数![]() 的解析式.
的解析式.
(![]() )若函数
)若函数![]() ,求函数
,求函数![]() 的最小值.
的最小值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线y2=2px(p>0)的焦点为F,已知点A,B为抛物线上的两个动点,且满足∠AFB=120°.过弦AB的中点M作抛物线准线的垂线MN,垂足为N,则 ![]() 的最大值为 .
的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:x0∈(0,+∞),3 ![]() +x0=2016,命题q:a∈(0,+∞),f(x)=|x|﹣ax,(x∈R)为偶函数,那么,下列命题为真命题的是( )
+x0=2016,命题q:a∈(0,+∞),f(x)=|x|﹣ax,(x∈R)为偶函数,那么,下列命题为真命题的是( )
A.p∧q
B.(¬p)∧q
C.p∧(¬q)
D.(¬p)∧(¬q)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(1,2),B(﹣3,﹣1),若圆x2+y2=r2(r>0)上恰有两点M,N,使得△MAB和△NAB的面积均为5,则r的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com