
【题目】对于棱长为![]() 的正方体
的正方体![]() ,有如下结论,其中错误的是( )
,有如下结论,其中错误的是( )
A. 以正方体的顶点为顶点的几何体可以是每个面都为直角三角形的四面体;
B. 过点![]() 作平面
作平面![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,则
,则![]() 三点共线;
三点共线;
C. 过正方体中心的截面图形不可能是正六边形;
D. 三棱锥![]() 与正方体的体积之比为
与正方体的体积之比为![]() .
.
科目:高中数学 来源: 题型:
【题目】设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为( )
A.y2=4x或y2=8x
B.y2=2x或y2=8x
C.y2=4x或y2=16x
D.y2=2x或y2=16x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系xOy中,过椭圆M: ![]() (a>b>0)右焦点的直线x+y﹣
(a>b>0)右焦点的直线x+y﹣ ![]() =0交M于A,B两点,P为AB的中点,且OP的斜率为
=0交M于A,B两点,P为AB的中点,且OP的斜率为 ![]() .
.
(1)求M的方程
(2)C,D为M上的两点,若四边形ACBD的对角线CD⊥AB,求四边形ACBD面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1 , ∠BAA1=60°. 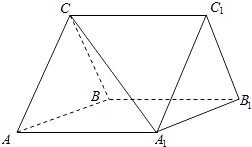
(1)证明AB⊥A1C;
(2)若平面ABC⊥平面AA1B1B,AB=CB,求直线A1C与平面BB1C1C所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图像向左平移
的图像向左平移![]() 个单位长度,再将图像上所有点的横坐标伸长到原来的
个单位长度,再将图像上所有点的横坐标伸长到原来的![]() 倍(纵坐标不变),得到
倍(纵坐标不变),得到![]() 的图像.
的图像.
(1)求![]() 的单调递增区间;
的单调递增区间;
(2)若对于任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com