
����Ŀ����ѧϰ����ʱ�����Ǿ����ˡ�ȷ�������ı���ʽ���ú���ͼ���о������ʡ������ú���������⡰��ѧϰ���̣��ڻ�����ͼ��ʱ������ͨ���б�����㡢���ߵķ�����������ѧ�ĺ���ͼ��ͬʱ������Ҳѧϰ������ֵ������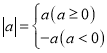 ��
��
������澭����ѧϰ���̣������������������⣺
�ں���![]() �У���
�У���![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ��
��

��1������������ı���ʽ��
��2���ڸ�����ƽ��ֱ������ϵ�У���ֱ�ӻ����˺�����ͼ��д������������������ʣ�
��3����ͼ����������![]() ��ͼ����������ĺ���ͼ��ֱ��д������ʽ
��ͼ����������ĺ���ͼ��ֱ��д������ʽ![]() �Ľ⼯��
�Ľ⼯��
���𰸡���1��![]() ����2��ͼ�����ʼ���������3��
����2��ͼ�����ʼ���������3��![]() ��
��
��������
��1������![]() ��
��![]() ��������뺯��
��������뺯��![]() �Ľ���ʽ�����
�Ľ���ʽ�����![]() ��
��![]() ��ֵ���ɴ˿ɵó��ú����Ľ���ʽ��
��ֵ���ɴ˿ɵó��ú����Ľ���ʽ��
��2����������ݣ�1���еı���ʽ���Ի����ú�����ͼ���ͼ��ɵó��ú����ĶԳ����뵥���ԣ�
��3�����������ͼ�����ֱ��д������ʽ�Ľ⼯��
��1������![]() ��
��![]() ��������뺯��
��������뺯��![]() �Ľ���ʽ����
�Ľ���ʽ����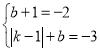 �����
�����![]() ,
,
���ԣ������Ľ���ʽΪ![]() ��
��
��2��ͼ�����£�
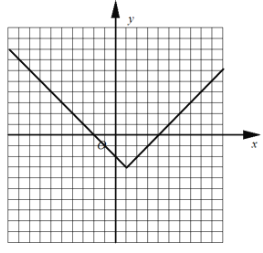
����![]() ��ͼ�����ֱ��
��ͼ�����ֱ��![]() �Գƣ��ú����ĵ����ݼ�����Ϊ
�Գƣ��ú����ĵ����ݼ�����Ϊ![]() ��������������Ϊ
��������������Ϊ![]() ����СֵΪ
����СֵΪ![]() ��
��
��3��ͼ�����£�

�۲�ͼ��ɵò���ʽ![]() �Ľ⼯Ϊ��
�Ľ⼯Ϊ��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������{an}���㵱n��1ʱ��an��![]() ����a1��
����a1��![]() .
.
(1)��֤������![]() Ϊ�Ȳ����У�
Ϊ�Ȳ����У�
(2)a1a2�Ƿ�������{an}�е������ǣ�����ǵڼ��������ǣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������������ʵ����
������������ʵ����![]() ������
������![]() ��ʹ
��ʹ![]() ��������Ƽ���
��������Ƽ���![]() ������ֱ�Ե㼯���������ĸ������У�������ֱ�Ե㼯�����ǣ� ��
������ֱ�Ե㼯���������ĸ������У�������ֱ�Ե㼯�����ǣ� ��
A.![]() B.
B.![]()
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ����������һ�ִ��͵��Ӳ�Ʒ���������ֲ�Ʒ����̶��ɱ�Ϊ2500��Ԫ��ÿ����![]() �ټ�������Ͷ��ɱ�
�ټ�������Ͷ��ɱ�![]() ����λ����Ԫ���������������30�ټ�ʱ��
����λ����Ԫ���������������30�ټ�ʱ��![]() �����������С��30�ټ�ʱ��
�����������С��30�ټ�ʱ��![]() ����ÿ�����Ӳ�Ʒ���ۼ�Ϊ5��Ԫ��ͨ���г�����������ҵ�����ĵ��Ӳ�Ʒ��ȫ��������.
����ÿ�����Ӳ�Ʒ���ۼ�Ϊ5��Ԫ��ͨ���г�����������ҵ�����ĵ��Ӳ�Ʒ��ȫ��������.
��1����������![]() ����Ԫ�����������
����Ԫ�����������![]() ���ټ����ĺ�����ϵʽ��
���ټ����ĺ�����ϵʽ��
��2�������Ϊ���ٰټ�ʱ������ҵ����һ���Ӳ�Ʒ�������л������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1��������![]() ����������ȵ�����㣬��
����������ȵ�����㣬��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��������![]() ��
��![]() �ϵ���СֵΪ-3����
�ϵ���СֵΪ-3����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
��![]() ����������Ϊ
����������Ϊ![]() ����a2=2b��
����a2=2b��
��1������Բ�ķ��̣�
��2��ֱ��l��x��y+m=0����Բ����A��B���㣬�Ƿ����ʵ��m��ʹ�߶�AB���е���Բx2+y2=5�ϣ������ڣ����m��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
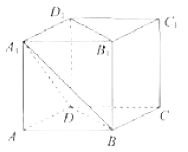
����Ŀ����ͼ����������![]() �У�
�У� ![]() ��ƽ��
��ƽ��![]() ����
����![]() ��ֱ��
��ֱ��![]() ����ƽ��
����ƽ��![]() �ظ����������ý�������Ϊ�� ��
�ظ����������ý�������Ϊ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������16���˿��ƣ�����![]() ��
��![]() ��4������
��4������![]() ��8��7��4��3��2���ݻ�
��8��7��4��3��2���ݻ�![]() ��
��![]() ��6��5��4������
��6��5��4������![]() ��5����ʦ����16����������һ�����������������Ƶĵ���������ѧ���ף��������ƵĻ�ɫ������ѧ���ң���ʱ����ʦ��ѧ����ѧ���ң������ܴ���֪�ĵ�����ɫ����֪��������ʲô�������ǣ���ʦ���������µĶԻ���ѧ���ף��Ҳ�֪�������ƣ�ѧ���ң���֪���㲻֪�������ƣ�ѧ���ף�������֪���������ˣ�ѧ���ң���Ҳ֪����.���������ǣ� ��
��5����ʦ����16����������һ�����������������Ƶĵ���������ѧ���ף��������ƵĻ�ɫ������ѧ���ң���ʱ����ʦ��ѧ����ѧ���ң������ܴ���֪�ĵ�����ɫ����֪��������ʲô�������ǣ���ʦ���������µĶԻ���ѧ���ף��Ҳ�֪�������ƣ�ѧ���ң���֪���㲻֪�������ƣ�ѧ���ף�������֪���������ˣ�ѧ���ң���Ҳ֪����.���������ǣ� ��
A. �ݻ�5B. ����![]()
C. ����4D. ����5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��[ѡ��4��4������ϵ���������]
��ֱ������ϵ![]() �У�����
�У�����![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() Ϊ��������ֱ��
Ϊ��������ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ��
��![]() ������.
������.
��1����![]() ��
��![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
��2��������![]() ��ֱ��
��ֱ��![]() �����߶ε��е�����Ϊ
�����߶ε��е�����Ϊ![]() ����
����![]() ��б�ʣ�
��б�ʣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com