
【题目】已知集合A={x|(x+3)(x﹣6)≥0},B={x| ![]() <0}.
<0}.
(1)求A∩RB;
(2)已知E={x|2a<x<a+1}(a∈R),若EB,求实数a的取值范围.
【答案】
(1)解:因为集合A={x|(x+3)(x﹣6)≥0}={x|x≤﹣3或x≥6},
B={x| ![]() <0}={x|(x+2)(x﹣14)<0}={x|﹣2<x<14};
<0}={x|(x+2)(x﹣14)<0}={x|﹣2<x<14};
RB={x|x≤﹣2或x≥14},
所以A∩RB={x|x≤﹣3或x≥14}
(2)解:因为E={x|2a<x<a+1}(a∈R),且EB,
所以分两种情况:
当E=时,2a≥a+1解得a≥1;
当E≠时,则2a<a+1且满足 ![]() 解得﹣1≤a<1;
解得﹣1≤a<1;
综上所述:实数a的取值范围是a≥﹣1
【解析】(1)化简集合A、B,求出RB与A∩RB即可;(2)由子集的定义,分E=和E≠时,求出实数a的取值范围即可.
【考点精析】掌握交、并、补集的混合运算是解答本题的根本,需要知道求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义域为(0,+∞)的单调函数,若对任意的x∈(0,+∞),都有f[f(x)﹣ ![]() ]=2,则f(2016)=( )
]=2,则f(2016)=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来空气质量逐步恶化,雾霾天气现象增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解心肺疾病是否与性别有关,在市第一人民医院随机对入院50人进行了问卷调查,得到如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | 20 | 5 | 25 |
女 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
(1)是否有99.5%的把握认为患心肺疾病与性别有关?说明你的理由;
(2)已知在患心肺疾病的10位女性中,有3位又患有胃病,现在从患心肺疾病的10位女性中,选出3位进行其他方面的排查,其中患胃病的人数为![]() ,求
,求![]() 的分布列、数学期望.
的分布列、数学期望.
参考公式: 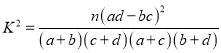 ,其中
,其中![]() .
.
下面的临界值仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设[x]表示不超过x的最大整数,如[1]=1,[0.5]=0,已知函数f(x)= ![]() ﹣k(x>0),若方程f(x)=0有且仅有3个实根,则实数k的取值范围是( )
﹣k(x>0),若方程f(x)=0有且仅有3个实根,则实数k的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ex(ax﹣1),g(x)=a(x﹣1),a∈R.
(1)讨论f(x)的单调性;
(2)若有且仅有两个整数xi(i=1,2),使得f(xi)<g(xi)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() 为自然对数的底数),
为自然对数的底数),![]() ,
, ![]() .
.
(1)若![]() 是
是![]() 的极值点,且直线
的极值点,且直线![]() 分别与函数
分别与函数![]() 和
和![]() 的图象交于
的图象交于![]() ,求
,求![]() 两点间的最短距离;
两点间的最短距离;
(2)若![]() 时,函数
时,函数![]() 的图象恒在
的图象恒在![]() 的图象上方,求实数
的图象上方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com