【题目】现有
六支足球队参加单循环比赛（即任意两支球队只踢一场比赛），第一周的比赛中
，各踢了
场， 
各踢了
场， 
踢了
场，且
队与
队未踢过， 
队与
队也未踢过，则在第一周的比赛中， 
队踢的比赛的场数是（ ）
A. 
B. 
C. 
D. 
科目：高中数学 来源： 题型：
【题目】第三届移动互联创新大赛，于2017年3月～10月期间举行，为了选出优秀选手，某高校先在计算机科学系选出一种子选手
，再从全校征集出3位志愿者分别与
进行一场技术对抗赛，根据以往经验， 
与这三位志愿者进行比赛一场获胜的概率分别为
，且各场输赢互不影响.
（1）求甲恰好获胜两场的概率；
（2）求甲获胜场数的分布列与数学期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某海产品经销商调查发现，该海产品每售出
吨可获利
万元，每积压
吨则亏损
万元.根据往年的数据，得到年需求量的频率分布直方图如图所示，将频率视为概率.
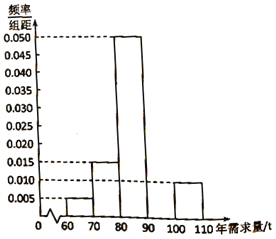
（1）请补齐
上的频率分布直方图，并依据该图估计年需求量的平均数；
（2）今年该经销商欲进货
吨，以
（单位：吨， 
）表示今年的年需求量，以
（单位：万元）表示今年销售的利润，试将
表示为
的函数解析式；并求今年的年利润不少于
万元的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】随着科学技术的飞速发展，手机的功能逐渐强大，很大程度上代替了电脑、电视.为了了解某高校学生平均每天使用手机的时间是否与性别有关，某调查小组随机抽取了
名男生、
名女生进行为期一周的跟踪调查，调查结果如表所示:
平均每天使用手机超过 | 平均每天使用手机不超过 | 合计 | |
男生 |
|
|
|
女生 |
|
|
|
合计 |
|
|
|
（1）能否在犯错误的概率不超过
的前提下认为学生使用手机的时间长短与性别有关？
（2）在这
名女生中，调查小组发现共有
人使用国产手机，在这
人中，平均每天使用手机不超过
小时的共有
人.从平均每天使用手机超过
小时的女生中任意选取
人，求这
人中使用非国产手机的人数
的分布列和数学期望.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式：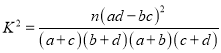 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，底面半径为
，母线长为
的圆柱的轴截面是四边形
，线段
上的两动点
， 
满足
.点
在底面圆
上，且
， 
为线段
的中点.
(Ⅰ)求证： 
平面
；
(Ⅱ)四棱锥
的体积是否为定值，若是，请求出该定值；若不是，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线
： 
的焦点为
，过点
的直线
交抛物线
于
（
位于第一象限）两点.
（1）若直线
的斜率为
，过点
分别作直线
的垂线，垂足分别为
，求四边形
的面积；
（2）若
，求直线
的方程.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
已知曲线
的参数方程为
（
为参数）.以直角坐标系的原点
为极点，
轴的正半轴为极轴建立坐标系，曲线
的极坐标方程为
.
（1）求的普通方程和的直角坐标方程；
（2）若过点
的直线
与交于
，
两点，与交于
，
两点，求
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
