
【题目】π为圆周率,e=2.718 28…为自然对数的底数.
(1)求函数f(x)=![]() 的单调区间;
的单调区间;
(2) 求e3,3e,eπ,πe,3π,π3这6个数中的最大数与最小数.
【答案】(1) 函数f(x)的单调递增区间为(0,e),单调递减区间为(e,+∞);(2) 最大数是3π,最小数是3e.
【解析】
(1)利用导数求函数f(x)=![]() 的单调区间.(2)先分析得到这6个数的最大数在π3与3π之中,最小数在3e与e3之中,再利用第1问的结论得到6个数中的最大数是3π,最小数是3e.
的单调区间.(2)先分析得到这6个数的最大数在π3与3π之中,最小数在3e与e3之中,再利用第1问的结论得到6个数中的最大数是3π,最小数是3e.
(1)函数f(x)的定义域为(0,+∞).
因为f(x)=![]() ,所以f′(x)=
,所以f′(x)=![]() .
.
当f′(x)>0,即0<x<e时,函数f(x)单调递增;
当f′(x)<0,即x>e时,函数f(x)单调递减.
故函数f(x)的单调递增区间为(0,e),单调递减区间为(e,+∞).
(2)因为e<3<π,所以eln 3<eln π,πln e<πln 3,即ln 3e<ln πe,ln eπ<ln 3π.
于是根据函数y=ln x,y=ex,y=πx在定义域上单调递增,可得3e<πe<π3,e3<eπ<3π.
故这6个数的最大数在π3与3π之中,最小数在3e与e3之中.
由e<3<π及(1)的结论,得f(π)<f(3)<f(e),
即![]() <
<![]() <
<![]() .
.
由![]() <
<![]() ,得ln π3<ln 3π,所以3π>π3;
,得ln π3<ln 3π,所以3π>π3;
由![]() <
<![]() ,得ln 3e<ln e3,所以3e<e3.
,得ln 3e<ln e3,所以3e<e3.
综上,6个数中的最大数是3π,最小数是3e.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
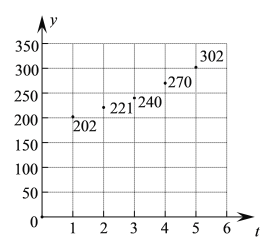
【题目】随着经济的发展和人民生活水平的提高,以及城市垃圾分类收集的实施和推广,我国居民生活垃圾的平均热值逐年.上升,垃圾焚烧发电的吨上网电量(单位:千瓦时/吨)显著增加.下表为某垃圾焚烧发电厂最近五个月的生产数据.
月份代码 |
|
|
|
|
|
吨上网电量 |
|
|
|
|
|
|
|
|
|
|
|
![]() 若从该发电厂这五个月的生产数据(吨上网电量)中任选两个,求其中至少有一个生产数据超过
若从该发电厂这五个月的生产数据(吨上网电量)中任选两个,求其中至少有一个生产数据超过![]() 的概率;
的概率;
![]() 通过散点图(如图)可以发现,变量
通过散点图(如图)可以发现,变量![]() 与
与![]() 之间的关系可以用函数
之间的关系可以用函数![]() (其中
(其中![]() 为自然对数的底数)来拟合,求常数
为自然对数的底数)来拟合,求常数![]() ,
,![]() 的值.
的值.
参考公式:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为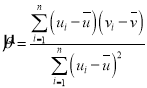 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费
(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费![]() 和年销售量
和年销售量![]() (
(![]() )数据作了初步处理,得到下面的散点图及一些统计量的值.
)数据作了初步处理,得到下面的散点图及一些统计量的值.

|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1.469 | 108.8 |
表中![]() ,
,![]()
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为年销售量y关于年宣传费x的回归方类型?给出判断即可,不必说明理由
哪一个适宜作为年销售量y关于年宣传费x的回归方类型?给出判断即可,不必说明理由
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;
(3)已知这种产品的年利润z与x、y的关系为![]() 根据(2)的结果回答下列问题:
根据(2)的结果回答下列问题:
①年宣传费![]() 时,年销售量及年利润的预报值是多少?
时,年销售量及年利润的预报值是多少?
②年宣传费x为何值时,年利润的预报值最大?
附:对于一组数据![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,原点为
,原点为![]() ,椭圆
,椭圆![]() 的动弦
的动弦![]() 过焦点
过焦点![]() 且不垂直于坐标轴,弦
且不垂直于坐标轴,弦![]() 的中点为
的中点为![]() ,过
,过![]() 且垂直于线段
且垂直于线段![]() 的直线交射线
的直线交射线![]() 于点
于点![]() .
.
(1)证明:点![]() 在定直线上;
在定直线上;
(2)当![]() 最大时,求
最大时,求![]() 的面积.
的面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 为参数),在以坐标原点
为参数),在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,点
轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若![]() 是曲线
是曲线![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点,求点
的中点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在一个实数![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的一个不动点,设函数
的一个不动点,设函数![]() (
(![]() ,
, ![]() 为自然对数的底数),定义在
为自然对数的底数),定义在![]() 上的连续函数
上的连续函数![]() 满足
满足![]() ,且当
,且当![]() 时,
时, ![]() .若存在
.若存在![]() ,且
,且![]() 为函数
为函数![]() 的一个不动点,则实数
的一个不动点,则实数![]() 的取值范围为( )
的取值范围为( )
A. 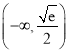 B.
B.  C.
C. 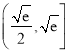 D.
D. 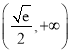
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴非负半轴为极轴建立极坐标系,已知直线
轴非负半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为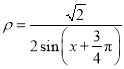 ,曲线
,曲线![]() 的参数方程为
的参数方程为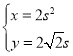 (
(![]() 为参数).
为参数).
(1)若直线![]() 平行于直线
平行于直线![]() ,且与曲线
,且与曲线![]() 只有一个公共点,求直线
只有一个公共点,求直线![]() 的方程;
的方程;
(2)若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某种气垫船的最大航速是![]() 海里小时,船每小时使用的燃料费用和船速的平方成正比.若船速为
海里小时,船每小时使用的燃料费用和船速的平方成正比.若船速为![]() 海里小时,则船每小时的燃料费用为
海里小时,则船每小时的燃料费用为![]() 元,其余费用(不论船速为多少)都是每小时
元,其余费用(不论船速为多少)都是每小时![]() 元。甲乙两地相距
元。甲乙两地相距![]() 海里,船从甲地匀速航行到乙地.
海里,船从甲地匀速航行到乙地.
(1)试把船从甲地到乙地所需的总费用![]() ,表示为船速
,表示为船速![]() (海里小时)的函数,并指出函数的定义域;
(海里小时)的函数,并指出函数的定义域;
(2)当船速为每小时多少海里时,船从甲地到乙地所需的总费用最少?最少费用为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com