
【题目】毕业季有![]() 位好友欲合影留念,现排成一排,如果:
位好友欲合影留念,现排成一排,如果:
(1)![]() 、
、![]() 两人不排在一起,有几种排法?
两人不排在一起,有几种排法?
(2)![]() 、
、![]() 两人必须排在一起,有几种排法?
两人必须排在一起,有几种排法?
(3)![]() 不在排头,
不在排头,![]() 不在排尾,有几种排法?
不在排尾,有几种排法?
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)试用“五点法”画出函数![]() 在区间
在区间![]() 的简图;
的简图;
(2)指出该函数的图象可由![]() 的图象经过怎样的平移和伸缩变换得到?
的图象经过怎样的平移和伸缩变换得到?
(3)若![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]() ,试求出函数
,试求出函数![]() 的最大值并指出
的最大值并指出![]() 取何值时,函数
取何值时,函数![]() 取得最大值.
取得最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将![]() 颗珠子分成
颗珠子分成![]() 堆.若通过每次从其中
堆.若通过每次从其中![]() 堆中各取走一颗珠子,而最后取完,则称这样的分法为“和谐的”.试给出和谐分法的充分必要条件,并加以证明.
堆中各取走一颗珠子,而最后取完,则称这样的分法为“和谐的”.试给出和谐分法的充分必要条件,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以直角坐标系的原点为极点,以
为参数),以直角坐标系的原点为极点,以![]() 轴的正半轴为极轴建立极坐标系,已知直线
轴的正半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)若![]() 与曲线
与曲线![]() 相切,且
相切,且![]() 与坐标轴交于
与坐标轴交于![]() 两点,求以
两点,求以![]() 为直径的圆的极坐标方程.
为直径的圆的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() 为平面
为平面![]() 内的一个有限点集,
内的一个有限点集, ![]() 为平面
为平面![]() 内的一个正三角形,集合
内的一个正三角形,集合![]() ,且
,且![]() .若对任意满足条件的集合S,均可以被正三角形
.若对任意满足条件的集合S,均可以被正三角形![]() 的两个平移图形覆盖,证明:集合
的两个平移图形覆盖,证明:集合![]() 可以被正三角形
可以被正三角形![]() 的两个平移图形覆盖.
的两个平移图形覆盖.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】凸多面体的每个面均为三角形,每条棱上均标记字母![]() 之一,且每个面的三条边上恰
之一,且每个面的三条边上恰![]() 各有一个。对每一个面,当旋转多面体使该面在我们眼前时,按照字母顺序
各有一个。对每一个面,当旋转多面体使该面在我们眼前时,按照字母顺序![]() 观察其三边,若是逆时针方向,则称其为正面;否则,称其为反面。证明:正面与反面的数目之差能被4整除。
观察其三边,若是逆时针方向,则称其为正面;否则,称其为反面。证明:正面与反面的数目之差能被4整除。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知焦点在![]() 轴上的抛物线
轴上的抛物线![]() 过点
过点![]() ,椭圆
,椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,其中
,其中![]() 与
与![]() 的焦点重合,过
的焦点重合,过![]() 与长轴垂直的直线交椭圆
与长轴垂直的直线交椭圆![]() 于
于![]() 两点且
两点且![]() ,曲线
,曲线![]() 是以原点为圆心以
是以原点为圆心以![]() 为半径的圆.
为半径的圆.
(1)求![]() 与
与![]() 及
及![]() 的方程;
的方程;
(2)若动直线![]() 与圆
与圆![]() 相切,且与
相切,且与![]() 交与
交与![]() 两点,三角形
两点,三角形![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
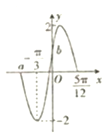
【题目】函数f(x)=Asin(2ωx+φ)(A>0,ω>0,|φ|<![]() )的部分图象如图所示
)的部分图象如图所示
(1)求A,ω,φ的值;
(2)求图中a,b的值及函数f(x)的递增区间;
(3)若α∈[0,π],且f(α)=![]() ,求α的值.
,求α的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com