
分析 (1)由圆的方程求出圆心和半径,易得点M在圆外,当切线的斜率不存在时,切线方程为x=3.当切线的斜率存在时,设切线的斜率为k,写出切线方程,利用圆心到直线的距离等于半径,解出k,可得切线方程.
(2)当直线AB的斜率不存在时,△ABC的面积S=3$\sqrt{7}$,当直线AB的斜率存在时,设直线AB的方程为y-3=k(x-1),即kx-y+3-k=0,圆心(-2,3)到直线AB的距离d=$\frac{|3k|}{\sqrt{{k}^{2}+1}}$,线段AB的长度|AB|=2$\sqrt{16-{d}^{2}}$,由此能求出△OAB的最大面积和此时直线AB的斜率.
解答 解:(1)圆C:x2+y2+4x-6y-3=0,即(x+2)2+(y-3)2=16,表示以(-2,3)为圆心,半径等于4的圆.
由于点M(-6,-5)到圆心的距离等于$\sqrt{(-2+6)^{2}+(3+5)^{2}}$=4$\sqrt{5}$,大于半径4,故点M在圆的外部.
当切线的斜率不存在时,切线方程为x=-6符合题意.
当切线的斜率存在时,设切线斜率为k,则切线方程为y+5=k(x+6),即kx-y+6k-5=0,
所以,圆心到切线的距离等于半径,即$\frac{|-2k-3+6k-5|}{\sqrt{{k}^{2}+1}}$=4,解得k=$\frac{3}{4}$,此时,切线为3x-4y-2=0.
综上可得,圆的切线方程为x=-6,或3x-4y-2=0.
(2)当直线AB的斜率不存在时,x=1,y=3±$\sqrt{7}$,△ABC的面积S=3$\sqrt{7}$
当直线AB的斜率存在时,设直线AB的方程为y-3=k(x-1),即kx-y+3-k=0,
圆心(-2,3)到直线AB的距离d=$\frac{|3k|}{\sqrt{{k}^{2}+1}}$,
线段AB的长度|AB|=2$\sqrt{16-{d}^{2}}$,
∴△ABC的面积S=$\frac{1}{2}$|AB|d=$\sqrt{{d}^{2}(16-{d}^{2})}$≤$\frac{{d}^{2}+(16-{d}^{2})}{2}$=8
当且仅当d2=8时取等号,此时$\frac{|3k|}{\sqrt{{k}^{2}+1}}$=2$\sqrt{2}$,解得k=±2$\sqrt{2}$.
所以,△OAB的最大面积为8,此时直线AB的斜率为±2$\sqrt{2}$.
点评 本题考查直线和圆的位置关系,具体涉及到圆的基本性质和圆的切线方程、三角形最大面积的求法和直线的斜率等知识点,注意切线的斜率不存在的情况,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{100},1)$ | B. | (0,$\frac{1}{100}$)∪(1,+∞) | C. | $(\frac{1}{100},100)$ | D. | (0,1)∪(100,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若事件A发生的概率为P(A),则0≤P(A)≤1 | |
| B. | 系统抽样是不放回抽样,每个个体被抽到的可能性相等 | |
| C. | 线性回归直线$\hat y=\hat bx+\hat a$必过点$(\overline x,\overline y)$ | |
| D. | 对于任意两个事件A和B,都有P(A∪B)=P(A)+P(B) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
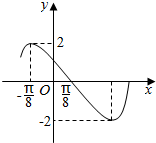 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示,则函数的解析式为( )
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的一段图象如图所示,则函数的解析式为( )| A. | y=2sin(2x-$\frac{π}{4}$) | B. | y=2sin(2x-$\frac{π}{4}$)或y=2sin(2x+$\frac{3π}{4}$) | ||
| C. | y=2sin(2x+$\frac{3π}{4}$) | D. | y=2sin(2x-$\frac{3π}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
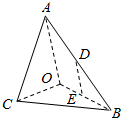 如图,在三棱锥AB0C中.AO⊥平面BOC,∠OAB=∠OAC=$\frac{π}{6}$.AB=AC=2.BC=$\sqrt{2}$,D,E分别为AB,OB的中点.
如图,在三棱锥AB0C中.AO⊥平面BOC,∠OAB=∠OAC=$\frac{π}{6}$.AB=AC=2.BC=$\sqrt{2}$,D,E分别为AB,OB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com