
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 分别为椭圆的左右焦点,点
分别为椭圆的左右焦点,点![]() 为椭圆
为椭圆![]() 上的一动点,
上的一动点,![]() 面积的最大值为2.
面积的最大值为2.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆
与椭圆![]() 的另一个交点为
的另一个交点为![]() ,点
,点![]() ,证明:直线
,证明:直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称.
轴对称.
科目:高中数学 来源: 题型:
【题目】如图两个同心球,球心均为点![]() ,其中大球与小球的表面积之比为3:1,线段
,其中大球与小球的表面积之比为3:1,线段![]() 与
与![]() 是夹在两个球体之间的内弦,其中
是夹在两个球体之间的内弦,其中![]() 两点在小球上,
两点在小球上,![]() 两点在大球上,两内弦均不穿过小球内部.当四面体
两点在大球上,两内弦均不穿过小球内部.当四面体![]() 的体积达到最大值时,此时异面直线
的体积达到最大值时,此时异面直线![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则![]() ( )
( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系
轴的正半轴为极轴建立极坐标系![]() ,极坐标系中
,极坐标系中![]() ,弧
,弧![]() 所在圆的圆心分别为
所在圆的圆心分别为![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() ,曲线
,曲线![]() 是弧
是弧![]() .
.
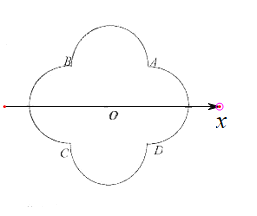
(1)分别写出![]() 的极坐标方程;
的极坐标方程;
(2)直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),点
为参数),点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 有两个不同交点
有两个不同交点![]() ,求实数
,求实数![]() 的取值范围,并求出
的取值范围,并求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】金秋九月,丹桂飘香,某高校迎来了一大批优秀的学生,新生接待其实也是和社会沟通的一个平台.校团委、学生会从在校学生中随机抽取了160名学生,对是否愿意投入到新生接待工作进行了问卷调查,统计数据如下:
愿意 | 不愿意 | |
男生 | 60 | 20 |
女生 | 40 | 40 |
(1)通过估算,试判断男、女哪种性别的学生愿意投入到新生接待工作的概率更大.
(2)能否有99%的把握认为,愿意参加新生接待工作与性别有关?
附: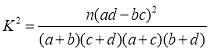 ,其中
,其中![]() .
.
| 0.05 | 0.01 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知从1开始的连续奇数蛇形排列形成宝塔形数表,第一行为1,第二行为3,5,第三行为7,9,11,第四行为13,15,17,19,如图所示,在宝塔形数表中位于第![]() 行,第
行,第![]() 列的数记为
列的数记为![]() ,比如
,比如![]() ,
,![]() ,
,![]() ,若
,若![]() ,则
,则![]() ( )
( )
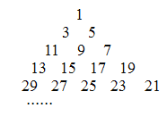
A.64B.65C.71D.72
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,平面
中,平面![]() 平面ABCD,
平面ABCD,![]() ,
,![]() ,底面ABCD是边长为2的菱形,点E,F分别为棱DC,BC的中点,点G是棱SC靠近点C的四等分点.
,底面ABCD是边长为2的菱形,点E,F分别为棱DC,BC的中点,点G是棱SC靠近点C的四等分点.
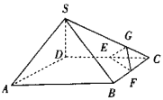
求证:(1)直线![]() 平面EFG;
平面EFG;
(2)直线![]() 平面SDB.
平面SDB.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的两顶点分别为
的两顶点分别为![]() ,
,![]() 为双曲线的一个焦点,
为双曲线的一个焦点,![]() 为虚轴的一个端点,若在线段
为虚轴的一个端点,若在线段![]() 上(不含端点)存在两点
上(不含端点)存在两点![]() ,使得
,使得![]() ,则双曲线的渐近线斜率
,则双曲线的渐近线斜率![]() 的平方的取值范围是( )
的平方的取值范围是( )
A.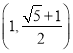 B.
B.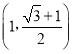 C.
C.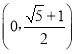 D.
D.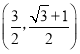
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com