
【题目】已知函数![]() .
.
(1)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)若![]() 是
是![]() 的唯一极值点,求
的唯一极值点,求![]() 的取值范围.
的取值范围.
【答案】(1)增区间是![]() ,减区间是
,减区间是![]() (2)
(2)![]()
【解析】
(1)利用导数![]() ,求函数的单调区间;
,求函数的单调区间;
(2)首先求函数的导数 ,令
,令![]() ,转化为函数
,转化为函数![]() 没有变号零点,求
没有变号零点,求![]() 的取值范围.
的取值范围.
解:(1)由题意可得![]()
![]()
当![]() 时,
时,![]() ,
,
因为![]() ,所以
,所以![]()
所以![]() 时,
时,![]() ,
,![]() 时,
时,![]() .
.
所以![]() 的增区间是
的增区间是![]() ,减区间是
,减区间是![]() .
.
(2) ,令
,令![]()
则![]() ,当
,当![]() ,
,![]() ,当
,当![]() ,
,![]() ,
,
所以![]() 在
在![]() 递减,在
递减,在![]() 递增,
递增,
所以![]()
①当![]() ,即
,即![]() 时,
时,![]() 恒成立,
恒成立,
故![]() 时,
时,![]() ;
;![]() 时,
时,![]()
故![]() 在
在![]() 递增,在
递增,在![]() 递减,所以
递减,所以![]() 是
是![]() 的唯一极值点,满足题意.
的唯一极值点,满足题意.
②当![]() .即
.即![]() 时,
时,![]() 在
在![]() 递减,在
递减,在![]() 递增,
递增,![]() .
.
故![]() 时,
时,![]() ,得
,得![]() ;
;![]() 时,
时,![]() ,得
,得![]()
故![]() 在
在![]() 递增,在
递增,在![]() 递减
递减
所以![]() 是
是![]() 的唯一极值点,满足题意.
的唯一极值点,满足题意.
③当![]() ,
,![]() 时,
时,![]() ,
,
![]() ,令
,令![]() ,则
,则![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,![]()
令![]() ,
,![]() ,
,![]() ,故
,故![]() 在
在![]() 递增,故
递增,故![]()
故![]() 在
在![]() 递增,
递增,![]() ,故
,故![]()
所以![]() 在
在![]() 存在唯一零点,设为
存在唯一零点,设为![]() ,
,
当![]() 时,
时,![]() ,得
,得![]() ;当
;当![]() 时,
时,![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 递减,
递减,![]() 递增,所以
递增,所以![]() 也是
也是![]() 的极值点,
的极值点,
所以![]() 不符合题意
不符合题意
综上所述,![]() 的取值范围是
的取值范围是![]()
(注:①②可合并)


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左,右焦点,直线
的左,右焦点,直线![]() 过点
过点![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,当直线
两点,当直线![]() 的斜率为
的斜率为![]() 时,线段
时,线段![]() 的长为
的长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一家公司生产某种品牌服装的年固定成本为![]() 万元,每生产
万元,每生产![]() 千件需另投入
千件需另投入![]() 万元.设该公司一年内共生产该品牌服装
万元.设该公司一年内共生产该品牌服装![]() 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为![]() 万元,且
万元,且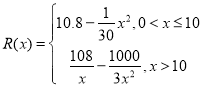 .
.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得利润最大?(注:年利润=年销售收入-年总成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
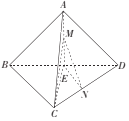
【题目】如图,在三棱锥A﹣BCD中,点E在BD上,EA=EB=EC=ED,BD![]() CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值
CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值![]() 时,三棱锥A﹣BCD的外接球的表面积为_____.
时,三棱锥A﹣BCD的外接球的表面积为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中,![]() ,前
,前![]() 项和为
项和为![]() ,若对任意的
,若对任意的![]() ,均有
,均有![]() (
(![]() 是常数,且
是常数,且![]() )成立,则称数列
)成立,则称数列![]() 为“
为“![]() 数列”.
数列”.
(1)若数列![]() 为“
为“![]() 数列”,求数列
数列”,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(2)若数列![]() 为“
为“![]() 数列”,且
数列”,且![]() 为整数,试问:是否存在数列
为整数,试问:是否存在数列![]() ,使得
,使得![]() 对任意
对任意![]() ,
,![]() 成立?如果存在,求出这样数列
成立?如果存在,求出这样数列![]() 的
的![]() 的所有可能值,如果不存在,请说明理由.
的所有可能值,如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com