
分析 可以求出$∠AOB=\frac{πt}{30}$,从而由余弦定理可以得到$d=10\sqrt{2(1-cos\frac{πt}{30})}=20\sqrt{si{n}^{2}\frac{πt}{60}}$,而由t∈[0,60]知,$sin\frac{πt}{60}≥0$,这样即可得出d=$20sin\frac{πt}{60}$.
解答 解:如图,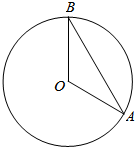
$∠AOB=\frac{t}{60}•2π=\frac{πt}{30}$;
∴由余弦定理得,$d=\sqrt{1{0}^{2}+1{0}^{2}-2•1{0}^{2}cos\frac{πt}{30}}$=$10\sqrt{2(1-cos\frac{πt}{30})}=10•2sin\frac{πt}{60}=20sin\frac{πt}{60}$.
故答案为:$20sin\frac{πt}{60}$.
点评 考查对钟表的认识,余弦定理用于求两点间的距离,以及二倍角的余弦公式,θ∈[0,π]时,sinθ≥0.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | [1,3] | B. | [2$\sqrt{2}$,3] | C. | [$\frac{6\sqrt{5}}{5}$,2$\sqrt{2}$] | D. | [$\frac{6\sqrt{5}}{5}$,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | [-1,+∞) | C. | [0,+∞) | D. | [1,+∞} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com