
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(Ⅱ)当![]() 时,讨论函数
时,讨论函数![]() 单调性;
单调性;
(Ⅲ)是否存在实数![]() ,对任意的
,对任意的![]() ,
, ![]() ,且
,且![]() ,有
,有![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【答案】(Ⅰ)![]() ;
; ![]() ; (Ⅱ)见解析;(Ⅲ)
; (Ⅱ)见解析;(Ⅲ) ![]() .
.
【解析】试题分析:(Ⅰ)当![]() 时,
时, ![]() ,求函数的导数,并且求
,求函数的导数,并且求![]() 的
的![]() 值,判断两侧的单调性,求极值;(Ⅱ)当
值,判断两侧的单调性,求极值;(Ⅱ)当![]() 时,
时, ![]() ,讨论两根
,讨论两根![]() 和
和![]() 的大小关系,从而得到函数的单调区间;(Ⅲ)设
的大小关系,从而得到函数的单调区间;(Ⅲ)设![]() ,将不等式整理为
,将不等式整理为![]() ,即说明函数
,即说明函数![]() 是单调递增函数,即
是单调递增函数,即![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
试题解析:(Ⅰ)当![]() 时,
时,
![]() ,
, ![]() .
.
当![]() 或
或![]() 时,
时, ![]() ,
, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,
, ![]() 单调递减,
单调递减,
所以![]() 时,
时, ![]() ;
;
![]() 时,
时, ![]() .
.
(Ⅱ)当![]() 时,
时, ![]()
![]()
![]() ,
,
①当![]() ,即
,即![]() 时,由
时,由![]() 可得
可得![]() 或
或![]() ,此时
,此时![]() 单调递增;由
单调递增;由![]() 可得
可得![]() ,此时
,此时![]() 单调递减;
单调递减;
②当![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上恒成立,此时
上恒成立,此时![]() 单调递增;
单调递增;
③当![]() ,即
,即![]() 时,由
时,由![]() 可得
可得![]() 或
或![]() ,此时
,此时![]() 单调递增;由
单调递增;由![]() 可得
可得![]() ,此时
,此时![]() 单调递减.
单调递减.
综上:当![]() 时,
时, ![]() 增区间为
增区间为![]() ,
, ![]() ,减区间为
,减区间为![]() ;
;
当![]() 时,
时, ![]() 增区间为
增区间为![]() ,无减区间;
,无减区间;
当![]() 时,
时, ![]() 增区间为
增区间为![]() ,
, ![]() ,减区间为
,减区间为![]() .
.
(Ⅲ)假设存在实数![]() ,对任意的
,对任意的![]() ,
, ![]() ,且
,且![]() ,有
,有![]() 恒成立,
恒成立,
不妨设![]() ,则由
,则由![]() 恒成立可得:
恒成立可得: ![]() 恒成立,
恒成立,
令![]() ,则
,则![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 恒成立,
恒成立,
即![]() 恒成立,
恒成立,
∴![]() ,即
,即![]() 恒成立,又
恒成立,又![]() ,
,
∴![]() 在
在![]() 时恒成立,
时恒成立,
∴![]() ,
,
∴当![]() 时,对任意的
时,对任意的![]() ,
, ![]() ,且
,且![]() ,有
,有![]() 恒成立.
恒成立.


科目:高中数学 来源: 题型:
【题目】选修4-4:极坐标与参数方程
已知平面直角坐标系![]() ,以
,以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() 为参数). 点
为参数). 点![]() 是曲线
是曲线![]() 上两点,点
上两点,点![]() 的极坐标分别为
的极坐标分别为![]() .
.
(1)写出曲线![]() 的普通方程和极坐标方程;
的普通方程和极坐标方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【天津市红桥区重点中学八校2017届高三4月联考数学(文)】已知椭圆![]() 的中心在原点,离心率等于
的中心在原点,离心率等于![]() ,它的一个短轴端点恰好是抛物线
,它的一个短轴端点恰好是抛物线![]() 的焦点
的焦点
(1)求椭圆![]() 的方程;
的方程;
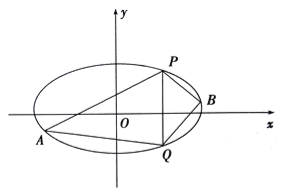
(2)已知![]() 、
、![]() 是椭圆上的两点,
是椭圆上的两点, ![]() ,
, ![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点.①若直线
两侧的动点.①若直线![]() 的斜率为
的斜率为![]() ,求四边形
,求四边形![]() 面积的最大值;
面积的最大值;
②当![]() ,
, ![]() 运动时,满足
运动时,满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由
的斜率是否为定值,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“丁香”和“小花”是好朋友,她们相约本周末去爬歌乐山,并约定周日早上8:00至8:30之间(假定她们在这一时间段内任一时刻等可能的到达)在歌乐山健身步道起点处会合,若“丁香”先到,则她最多等待“小花”15分钟.若“小花”先到,则她最多等待“丁香”10分钟,若在等待时间内对方到达,则她俩就一起快乐地爬山,否则超过等待时间后她们均不再等候对方而孤独爬山,则“丁香”和“小花”快乐地一起爬歌乐山的概率是(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是梯形.四边形
是梯形.四边形![]() 是矩形.且平面
是矩形.且平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上的动点.
上的动点.
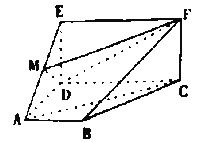
(Ⅰ)试确定点![]() 的位置,使
的位置,使![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(Ⅱ)在(Ⅰ)的条件下,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四个函数y=sin|x|,y=cos|x|,y= ![]() ,y=lg|sinx|中,以π为周期,在
,y=lg|sinx|中,以π为周期,在 ![]() 上单调递增的偶函数是( )
上单调递增的偶函数是( )
A.y=sin|x|
B.y=cos|x|
C.y= ![]()
D.y=lg|sinx|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】写出下列命题的否定,并判断其真假:
(1)p:不论m取何实数,方程x2+x-m=0必有实数根;
(2)q:存在一个实数x,使得x2+x+1≤0;
(3)r:等圆的面积相等,周长相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com