
分析 (1)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(2)求出g(x)的导数,设出切点坐标,表示出切线方程,求出关于a的解析式,根据函数的单调性求出a的范围即可.
解答 解:(1)由已知得:f'(x)=[ax2+(2a+1)x]ex=[x(ax+2a+1)]ex.
①若$-\frac{1}{2}<a<0$,当$x>-2-\frac{1}{a}$或x<0时,f'(x)<0;当$0<x<-2-\frac{1}{a}$时,f'(x)>0,
所以f(x)的单调递增区间为$({0,-2-\frac{1}{a}})$;单调递减区间为$({-∞,0}),({-2-\frac{1}{a},+∞})$.
②若$a=-\frac{1}{2},f'(x)=-\frac{1}{2}{x^2}{e^x}≤0$,故f(x)的单调递减区间为(-∞,+∞);
③若$a<-\frac{1}{2}$,当$x<-2-\frac{1}{a}$或x>0时,f'(x)<0;当$-2-\frac{1}{a}<x<0$时,f'(x)>0;
所以f(x)的单调递增区间为$({-2-\frac{1}{a},0})$;单调递减区间为$({-∞,-2-\frac{1}{a}}),({0,+∞})$.
综上,当$-\frac{1}{2}<a<0$时,f(x)单调递增区间为$({0,-2-\frac{1}{a}})$;单调递减区间为(-∞,0),$({-2-\frac{1}{a},+∞})$.
当$a=-\frac{1}{2}$时,f(x)的单调递减区间为(-∞,+∞);
当$a<-\frac{1}{2}$时,f(x)单调递增区间为$({-2-\frac{1}{a},0})$;单调递减区间为$({-∞,-2-\frac{1}{a}})$,(0,+∞).
(2)证明:$g(x)=a{x^2}+x+lnx-1,g'(x)=\frac{{2a{x^2}+x+1}}{x}$,
设切点$({{x_0},a{x_0}^2+{x_0}+ln{x_0}-1})$,斜率为$\frac{{2a{x_0}^2+{x_0}+1}}{x_0}=-e$①,
所以切线方程为$y-({a{x_0}^2+{x_0}+ln{x_0}-1})=\frac{{a{x_0}^2+{x_0}+1}}{x_0}(x-{x_0})$,
将(0,0)代入得:$-({a{x_0}^2+{x_0}+ln{x_0}-1})=e{x_0}$②,
由 ①知$a=\frac{{-e{x_0}-{x_0}-1}}{{2{x_0}^2}}$代入②得:(e+1)x0+2lnx0-3=0,令u(x)=(e+1)x+2lnx-3,
则$u'(x)=e+1+\frac{2}{x}>0$恒成立,∴u(x)在(0,+∞)单增,且$u(1)=e-2>0,u({\frac{1}{e}})<0$,
∴$\frac{1}{e}<{x_0}<1$,∴$a=\frac{{e{x_0}-{x_0}-1}}{{2{x_0}^2}}=-\frac{1}{2}{({\frac{1}{x_0}})^2}-\frac{e+1}{2}({\frac{1}{x_0}})$,
令$t=\frac{1}{x_0}$,则1<t<e,则$a(t)=-\frac{1}{2}{t^2}-\frac{e+1}{2}t$
在(1,e)递减,且$a(1)=-\frac{e+2}{2},a(e)=-\frac{{2{e^2}+e}}{2}$,
∴$-\frac{{2{e^2}+e}}{2}<a<-\frac{e+2}{2}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
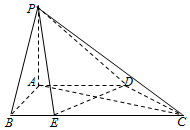 如图,在四棱锥P-ABCD中,AD∥BC,AB⊥AD,PA⊥平面ABCD,点E在BC上,BC=2AB=2AD=4BE.
如图,在四棱锥P-ABCD中,AD∥BC,AB⊥AD,PA⊥平面ABCD,点E在BC上,BC=2AB=2AD=4BE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | ①②③ | B. | ②③④ | C. | ②④⑤ | D. | ③④⑤ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{3}$ | B. | 6 | C. | 8 | D. | 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com