Question

6．设抛物线$\left\{\begin{array}{l}{x=2p{t}^{2}}\\{y=2pt}\end{array}\right.$（t为参数，p＞0）的焦点为F（1，0），过F的直线与抛物线交于A，B两点，且满足|AF|=3|BF|，则弦AB的中点到准线的距离为$\frac{8}{3}$．

Answer 1

分析 设|BF|=m，由抛物线的定义知AA₁和BB₁，进而可推断出AC和AB，及直线AB的斜率，则直线AB的方程可得，与抛物线方程联立消去y，进而跟韦达定理求得x₁+x₂的值，则根据抛物线的定义求得弦AB的中点到准线的距离．

解答 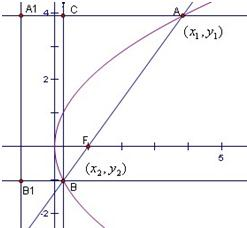解：抛物线$\left\{\begin{array}{l}{x=2p{t}^{2}}\\{y=2pt}\end{array}\right.$（t为参数，p＞0）的焦点为F（1，0），普通方程为y²=4x，
设|BF|=m，由抛物线的定义知
|AA₁|=3m，|BB₁|=m
∴△ABC中，|AC|=2m，|AB|=4m，k_AB=$\sqrt{3}$
直线AB方程为y=$\sqrt{3}$（x-1）
与抛物线方程联立消y得3x²-10x+3=0
所以AB中点到准线距离为$\frac{5}{3}$+1=$\frac{8}{3}$．
故答案为：$\frac{8}{3}$

点评 本题主要考查了抛物线的简单性质．考查了直线与抛物线的关系及焦点弦的问题．常需要利用抛物线的定义来解决．