(Ⅰ)解:求导函数可得:f′(x)=lnx+1(x>0)
令f′(x)≥0,即lnx≥-1,∴x

;令f′(x)≤0,即lnx≤-1,∴0<x
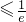
;
∴f(x)单调递增区间为[

,+∞),单调递减区间为(0,

]
∴f(x)
min=f(

)=-

(Ⅱ)解:F(x)=

=

,求导函数可得F′(x)=

当a≥0时,F′(x)>0,F(x)在[1,e]上单调递增,F(x)
min=-a=

,∴a=-

∉[0,+∞),舍去;
当a<0时,F(x)在(0,-a)单调递减,在(-a,+∞)单调递增
若a∈(-1,0),F(x)在[1,e]上单调递增,F(x)
min=-a=

,∴a=-

∉(-1,0),舍去;
若a∈[-e,-1],F(x)在(1,-a)单调递减,在(-a,e)单调递增,
∴F(x)
min=F(-a)=ln(-a)+1=

,∴a=-
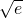
∈[-e,-1];
若a∈(-∞,-1),F(x)在[1,e]上单调递减,∴F(x)
min=F(e)=-
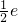
∉(-∞,-1),舍去;
综上所述:a=-
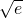
(Ⅲ)证明:由(I)可知当b>0时,有f(b)≥f(x)
min=f(

)=-

,∴

,
即


.
∴

分析:(Ⅰ)求导函数,令f′(x)≥0,确定函数的单调递增区间;令f′(x)≤0,确定函数的单调递减区间,从而可求函数的最小值;
(Ⅱ)F(x)=

=

,求导函数可得F′(x)=

,分类讨论,确定函数的单调性,利用函数在[1,e]上是最小值为

,可求a的值;
(Ⅲ)由(I)可知当b>0时,有f(b)≥f(x)
min=f(

)=-

,所以

,从而可知结论成立.
点评:本试题考查了导数在研究函数中的运用,求函数的最值,以及结合不等式的知识证明不等式的成立.解决该试题的关键是第一问能利用导数求出参数a的值,并能利用第一问来递进式解决第二问.

 在[1,e]上是最小值为
在[1,e]上是最小值为 ,求a的值;
,求a的值; (其中e=2.718 28…是自然对数的底数).
(其中e=2.718 28…是自然对数的底数). ;令f′(x)≤0,即lnx≤-1,∴0<x
;令f′(x)≤0,即lnx≤-1,∴0<x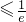 ;
; ,+∞),单调递减区间为(0,
,+∞),单调递减区间为(0, ]
] )=-
)=-
 =
= ,求导函数可得F′(x)=
,求导函数可得F′(x)=
 ,∴a=-
,∴a=- ∉[0,+∞),舍去;
∉[0,+∞),舍去; ,∴a=-
,∴a=- ∉(-1,0),舍去;
∉(-1,0),舍去; ,∴a=-
,∴a=-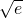 ∈[-e,-1];
∈[-e,-1];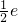 ∉(-∞,-1),舍去;
∉(-∞,-1),舍去;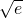
 )=-
)=- ,∴
,∴ ,
,
 .
.
 =
= ,求导函数可得F′(x)=
,求导函数可得F′(x)= ,分类讨论,确定函数的单调性,利用函数在[1,e]上是最小值为
,分类讨论,确定函数的单调性,利用函数在[1,e]上是最小值为 ,可求a的值;
,可求a的值; )=-
)=- ,所以
,所以 ,从而可知结论成立.
,从而可知结论成立.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案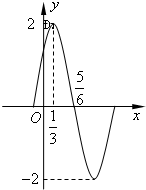 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<