
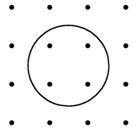
错解1:16个点中任取3个有![]() 种方法,其中三个点都不在圆内的有
种方法,其中三个点都不在圆内的有![]() 种,故满足题设条件的三角形有
种,故满足题设条件的三角形有![]() -
-![]() =340个.
=340个.
错解2:要作出符合题意的三角形,从圆内四点中:
①任取3点,有![]() 种;
种;
②任取2点,圆外取1点,有![]()
![]() 种;
种;
③任取1点,圆外取2点,有![]()
![]() 种.
种.
综上可知,至少有一个顶点在圆内的三角形共有![]() +
+![]()
![]() +
+![]()
![]() =340个.
=340个.
剖析:错解1中不符合题意的还有两种情形:一是4点共线,但其中任意3点至少有1点在圆内,这样的4点有6种;还有就是只有3点共线,但其中恰有1点在圆内,这样的3点有4种.因此,正确解法是:![]() -
-![]() -6
-6![]() -4
-4![]() =312种.
=312种.
错解2错在②③两种情形,其中所取的3点可能是共线的.因此,要兼顾题中的两个约束条件:所取三点可作成三角形;至少有一个点在圆内.因此正确解法是:从圆内四点中任取.
①3点,有![]() 种;
种;
②2点,圆外12点中取1点,有![]()
![]() 种;
种;
③1点,圆外12点中取2点,有![]() (
(![]() -4)种.
-4)种.
综上可知,所求的三角形共有![]() +
+![]()
![]() +
+![]() (
(![]() -4)=312个.
-4)=312个.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com