设Sn是等比数列{an}的前n项和,
(1)若S3,S9,S6成等差数列,求证:a2,a8,a5成等差数列.
(2)设p,r,t,k,m,n∈N*,且p,r,t成等差数列,若pSk,rSm,tSn成等差数列,试判断pak+1,ram+1,tan+1三者关系,并说明理由.
【答案】
分析:(1)设{a
n}的公比为q,根据等比数列的前n项和公式及2S
9=S
6+S
3,建立关于q的方程解出q
3=-

,从而化简得a
2+a
5-2a
8=0,所以a
2,a
8,a
5成等差数列.
(2)根据题意,可得2rS
m=pS
k+tS
n,当q=1时,结合2r=p+t不难推出2ra
m+1=pa
k+1+ta
n+1成立,即pa
k+1,ra
m+1,ta
n+1成等差数列.当q≠1时,根据等比数列的通项与求和公式,化简等式2rS
m=pS
k+tS
n得到2ra
1q
m=pa
1q
k+ta
1q
n,即2ra
m+1=pa
k+1+ta
n+1.由此可得若pS
k,rS
m,tS
n成等差数列,则pa
k+1,ra
m+1,ta
n+1成等差数列.
解答:解:(1)依题意,设等比数列{a
n}的公比为q,
可得2S
9=S
6+S
3,即2

=

+

整理得2q
6-q
3-1=0,解q
3=1或-

,
∵q=1时,2S
9=S
6+S
3不成立
∴q
3=-

,
可得a
2+a
5-2a
8=a
2(1+q
3-2q
6)=a
2(1-

-2×

)=0
∴a
2+a
5=2a
8,即a
2,a
8,a
5成等差数列.
(2)设等比数列{a
n}的公比为q,
由pS
k,rS
m,tS
n成等差数列,可得2rS
m=pS
k+tS
n,
当q=1时,a
k+1=a
m+1=a
n+1=a
1,结合2r=p+t得到2ra
m+1=pa
k+1+ta
n+1.
当q≠1时,由2rS
m=pS
k+tS
n结合等比数列前n项和公式,
化简得2ra
1(1-q
m)=pa
1(1-q
k)+ta
1(1-q
n),
∵2r=p+t,可得2ra
1=pa
1+ta
1,
∴上式化简,得2ra
1q
m=pa
1q
k+ta
1q
n,即2ra
m+1=pa
k+1+ta
n+1.
综上所述,若pS
k,rS
m,tS
n成等差数列,则pa
k+1,ra
m+1,ta
n+1成等差数列.
点评:本题给出等比数列满足的条件,探索pa
k+1,ra
m+1,ta
n+1是否成等差数列的问题.着重考查了等比数列的通项公式、求和公式和等差数列、等比数列之间的关系等知识,属于中档题.

 ,从而化简得a2+a5-2a8=0,所以a2,a8,a5成等差数列.
,从而化简得a2+a5-2a8=0,所以a2,a8,a5成等差数列. =
= +
+
 ,
, ,
, -2×
-2× )=0
)=0

 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案 ,则
,则 等于( )
等于( )



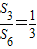 ,则
,则 等于( )
等于( )


