练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知圆C：x2+y2-4x-14y+45=0及点Q(-2,3).

    (1)若点P(m,m+1)在圆C上，求直线PQ的斜率.

    (2)若M是圆C上任一点，求|MQ|的取值范围.

    (3)若点N(a,b)在圆C上，求的最大值与最小值.

    【答案】（1）；（2）≤|MQ|≤；（3）umax=2+,umin=2-.

    【解析】

    (1)根据点P在圆上求出m的值，再求直线PQ的斜率.(2)利用数形结合求|MQ|的取值范围.（3）利用斜率的几何意义和数形结合求的最大值与最小值.

    (1)∵P在圆C上，

    ∴m2+(m+1)2-4m-14(m+1)+45=0,

    ∴m=4,即P(4,5).∴kPQ=.

    (2)∵圆心C(2，7)，半径r=，|CQ|=,

    ∴≤|MQ|≤.

    (3)表示点N(a,b)与定点(-2,3)连线斜率，

    当直线y-3=u(x+2)与圆C相切时，取得值u=2±,

    ∴umax=2+,umin=2-.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】二次函数f(x)满足f(x＋1)－f(x)＝2x，且f(0)＝1.

    (1)求f(x)的解析式；

    (2)解不等式f(x)＞2x＋5.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C的对称中心为原点O，焦点在x轴上，离心率为，且点在该椭圆上。

    （I）求椭圆C的方程；

    （II）过椭圆C的左焦点的直线l与椭圆C相交于两点，若的面积为，求圆心在原点O且与直线l相切的圆的方程。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的一个焦点为，离心率为.点为圆上任意一点， 为坐标原点.

    （1）求椭圆的标准方程；

    （2）设直线经过点且与椭圆相切， 与圆相交于另一点，点关于原点的对称点为，证明：直线与椭圆相切.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆，为坐标原点，动点在圆外，过点作圆的切线，设切点为.

    （1）若点运动到处，求此时切线的方程；

    （2）求满足的点的轨迹方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】做一个无盖的圆柱形水桶，若要使其体积是，且用料最省，则圆柱的底面半径为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】△ABC的顶点A的坐标为(1,4)，∠B，∠C的平分线所在直线方程分别为x－2y＝0和x＋y－1＝0，求BC所在直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2015年我国将加快阶梯水价推行，原则是“保基本、建机制、促节约”，其中“保基本”是指保证至少80%的居民用户用水价格不变．为响应国家政策，制定合理的阶梯用水价格，某城市采用简单随机抽样的方法分别从郊区和城区抽取5户和20户居民的年人均用水量进行调研，抽取的数据的茎叶图如下（单位：吨）：

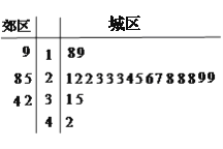
    （1）在郊区的这5户居民中随机抽取2户，求其年人均用水量都不超过30吨的概率；

    （2）设该城市郊区和城区的居民户数比为，现将年人均用水量不超过30吨的用户定义为第一阶梯用户，并保证这一梯次的居民用户用水价格保持不变．试根据样本估计总体的思想，分析此方案是否符合国家“保基本”政策．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆： 的离心率为，且过点， ， 是椭圆上异于长轴端点的两点.

    （1）求椭圆的方程；

    （2）已知直线： ，且，垂足为， ，垂足为，若，且的面积是面积的5倍，求面积的最大值.

    查看答案和解析>>

    同步练习册答案