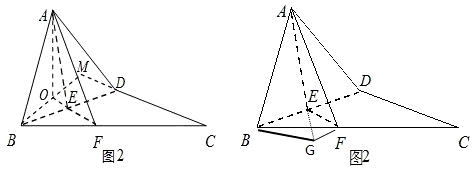
证明:(Ⅰ)在△ABC中,由∠ACB=30°,得
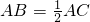
.
由D为AC的中点,得
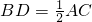
.∴△ABD为等边三角形
则BD⊥AE,BD⊥EF,
∴BD⊥面AEF,
又∵BD?面BCD,∴面AEF⊥面BCD.
同理面AEF⊥面BAD…
(Ⅱ)由(Ⅰ)的证明可得∠AEF为二面角A-BD-C的平面角.过A作AO⊥面BCD,垂足为O.
∵面AEF⊥面BCD,∴O在FE上,连BO交CD延长线于M,
当AB⊥CD时,由三垂线定理的逆定理得BM⊥CM,
∴O为翻折前的等边三角形△ABD的中心.
则
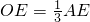
,
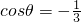
.
因此当
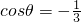
时,AB⊥CD.…(7分)
(Ⅲ)过F作FG⊥AE交AE的延长线于G点,由(Ⅰ)面AEF⊥面BAD,则FG⊥面BAD
故∠FBG就是FA与平面BAD所成角
设AB=a,则
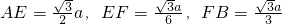
;
而
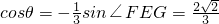
,
故
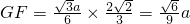
所以
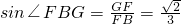
即FB与平面BAD所成角的正弦值为

…(12分)
分析:(Ⅰ)可以先证明△ABD为等边三角形,从而可得BD⊥AE,BD⊥EF,根据线面垂直的判定可得BD⊥面AEF,进而根据面面垂直的判定可得面AEF⊥面BCD.同理面AEF⊥面BAD
(Ⅱ)由(Ⅰ)的证明可得∠AEF为二面角A-BD-C的平面角.过A作AO⊥面BCD,垂足为O.由于面AEF⊥面BCD,所以O在FE上,连BO交CD延长线于M,从而当AB⊥CD时,由三垂线定理的逆定理得BM⊥CM,由此可求得cosθ的值;
(Ⅲ)过F作FG⊥AE交AE的延长线于G点,由(Ⅰ)面AEF⊥面BAD,则FG⊥面BAD,故∠FBG就是FA与平面BAD所成角,在三角形FBG中,可求∠FBG的正弦值.
点评:本题以平面图形为载体,考查图形的翻折,关键是搞清翻折前后有关元素的变与不变,考查面面角,考查线面角,关键是正确作出相应的角.


 证明:(Ⅰ)在△ABC中,由∠ACB=30°,得
证明:(Ⅰ)在△ABC中,由∠ACB=30°,得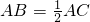 .
.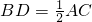 .∴△ABD为等边三角形
.∴△ABD为等边三角形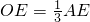 ,
,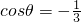 .
.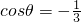 时,AB⊥CD.…(7分)
时,AB⊥CD.…(7分)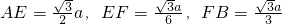 ;
;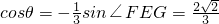 ,
,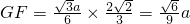
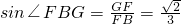
 …(12分)
…(12分)


