
分析 用$\overrightarrow{AB},\overrightarrow{AC}$表示出$\overrightarrow{CD}$,解出p,q.
解答 解:$\overrightarrow{CD}$=$\frac{2}{3}$$\overrightarrow{CB}$=$\frac{2}{3}$($\overrightarrow{AB}-\overrightarrow{AC}$)=$\frac{2}{3}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AC}$,
∴p=$\frac{2}{3}$,q=-$\frac{2}{3}$,∴p+q=0.
故答案为:0.
点评 本题考查了平面向量的基本定理及几何意义,是基础题.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m⊥l,n⊥l,则m∥n | B. | α⊥γ,β⊥γ,则α⊥β | C. | m∥α,n∥α,则m∥n | D. | α∥γ,β∥γ,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
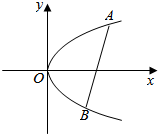 已知抛物线C的方程为y2=2px(p>0),一条长度为4p的线段AB的两个端点A、B在抛物线C上运动,则线段AB的中点D到y轴距离的最小值为 ( )
已知抛物线C的方程为y2=2px(p>0),一条长度为4p的线段AB的两个端点A、B在抛物线C上运动,则线段AB的中点D到y轴距离的最小值为 ( )| A. | 2p | B. | $\frac{5}{2}p$ | C. | $\frac{3}{2}p$ | D. | 3p |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
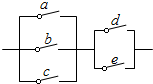 如图,a,b,c,d,e是处于断开状态的开关,任意闭合两个,则电路被接通的概率是( )
如图,a,b,c,d,e是处于断开状态的开关,任意闭合两个,则电路被接通的概率是( )| A. | $\frac{2}{5}$ | B. | $\frac{3}{20}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com