
【题目】某班对一次实验成绩进行分析,利用随机数表法抽取样本时,先将50个同学按01,02.03,…50进行编号,然后从随机数表第9行第11列的数开始向右读,则选出的第6个个体是( )(注:表为随机数表的第8行和第9行)
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
A.00B.13C.42D.44
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:
【题目】国家统计局统计了我国近10年(2009年2018年)的GDP(GDP是国民经济核算的核心指标,也是衡量一个国家或地区总体经济状况的重要指标)增速的情况,并绘制了下面的折线统计图.
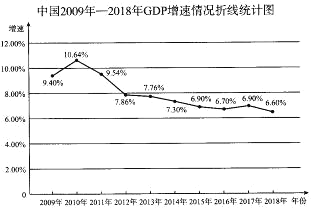
根据该折线统计图,下面说法错误的是
A. 这10年中有3年的GDP增速在9.00%以上
B. 从2010年开始GDP的增速逐年下滑
C. 这10年GDP仍保持6.5%以上的中高速增长
D. 2013年—2018年GDP的增速相对于2009年—2012年,波动性较小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划投资开发一种新能源产品,预计能获得10万元![]() 1000万元的收益.现准备制定一个对开发科研小组的奖励方案:奖金
1000万元的收益.现准备制定一个对开发科研小组的奖励方案:奖金![]() (单位:万元)随收益
(单位:万元)随收益![]() (单位:万元)的增加而增加,且奖金总数不超过9万元,同时奖金总数不超过收益的
(单位:万元)的增加而增加,且奖金总数不超过9万元,同时奖金总数不超过收益的![]() .
.
(Ⅰ)若建立奖励方案函数模型![]() ,试确定这个函数的定义域、值域和
,试确定这个函数的定义域、值域和![]() 的范围;
的范围;
(Ⅱ)现有两个奖励函数模型:①![]() ;②
;②![]() .试分析这两个函数模型是否符合公司的要求?请说明理由.
.试分析这两个函数模型是否符合公司的要求?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,其焦距为
,其焦距为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上,![]() ,直线
,直线![]() 的斜率为
的斜率为![]() (
(![]() 为半焦距)·
为半焦距)·
(1)求椭圆![]() 的方程;
的方程;
(2)设圆![]() 的切线
的切线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(
两点(![]() 为坐标原点),求证:
为坐标原点),求证:![]() ;
;
(3)在(2)的条件下,求![]() 的最大值
的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]() ,
,![]() .
.
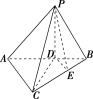
(1)求证:![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成的锐二面角.
所成的锐二面角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】参加衡水中学数学选修课的同学,对某公司的一种产品销量与价格进行统计,得到如下数据和散点图:
定价 |
|
|
|
|
|
|
年销售 |
|
|
|
|
|
|
|
|
|
|
|
|
|
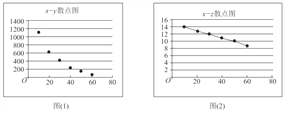
(参考数据:![]()
![]() )
)
(I)根据散点图判断,![]() 与
与![]() ,
,![]() 与
与![]() 哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
(II)根据(I)的判断结果有数据,建立![]() 关于
关于![]() 的回归方程(方程中的系数均保留两位有效数字);
的回归方程(方程中的系数均保留两位有效数字);
(III)定价为多少元/![]() 时,年利润的预报值最大?
时,年利润的预报值最大?
附:对一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: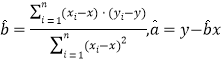 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年,某地认真贯彻落实中央十九大精神和各项宏观调控政策,经济运行平稳增长,民生保障持续加强,惠民富民成效显著,城镇居民收入稳步增长,收入结构稳中趋优.据当地统计局公布的数据,现将8月份至12月份当地的人均月收入增长率与人均月收入分别绘制成折线图(如图一)与不完整的条形统计图(如图二).请从图中提取相关的信息:
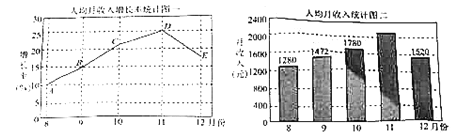
①10月份人均月收入增长率为![]() 左右;
左右;
②11月份人均月收入为2047元;
③从上图可知该地9月份至12月份人均月收入比8月份人均月收入均得到提高.
其中正确的信息个数为( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com